题目内容
18．函数f（x）=（$\frac{1}{2}$）x-log2x的零点个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 将方程的解的个数转化为两个函数的交点问题，通过图象即可解答．
解答 
解：函数f（x）=（$\frac{1}{2}$）x-log2x的零点个数，是方程log2x-（$\frac{1}{2}$）x=0的实数根的个数，
即log2x=（$\frac{1}{2}$）x，
令f（x）=log2x，g（x）=（$\frac{1}{2}$）x，
画出函数的图象，如图所示：
由图象得：f（x）与g（x）有1个交点，
∴函数f（x）=（$\frac{1}{2}$）x-log2x的零点个数为1个，
故选：B．
点评 本题考查了函数零点的应用问题，也考查了转化思想，数形结合思想的应用问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．已知为{an}等差数列，且a2=2，a3=-4，则公差d=（ ）
| A． | 27 | B． | -11 | C． | -6 | D． | 3 |
6．一项针对人们休闲方式的调查结果如下：受调查对象总计124人，其中女性70人，男性54人．女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动．
（1）根据以上数据建立一个2×2的列联表；
（2）根据下列提供的独立检验临界值表，你最多能有多少把握认为性别与休闲方式有关系？
独立检验临界值表：
参考公式：K2=$\frac{n（ad-bc）}{（a+b）（c+d）（a+c）（b+d）}$．
（1）根据以上数据建立一个2×2的列联表；
（2）根据下列提供的独立检验临界值表，你最多能有多少把握认为性别与休闲方式有关系？
独立检验临界值表：
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13．甲乙两台机床同时生产一种零件，10天中，两台机床每天出的次品数分别是
由此判断性能较好的一台是乙．
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
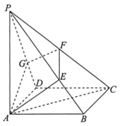如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA丄底面ABCD，PA=AC．过点A的平面与棱PB，PC，PD分别交于点E，F，G（E，F，G三点均不在棱的端点处）．
如图：三棱柱ABC-A1B1C1中，AA1⊥平面ABC，BC⊥AC，M是AB上的动点，CB=CA=CC1=2．