题目内容
9.在平面四边形ABCD中,E为BC的中点,且EA=1,ED=$\sqrt{3}$.若$\overrightarrow{AB}$•$\overrightarrow{AC}$=-1,则$\overrightarrow{BD}$•$\overrightarrow{DC}$的值是-1.分析 以E为原点建立坐标系,设出各点坐标,根据条件列方程,得出B点坐标,代入向量的数量积公式化简即可.
解答 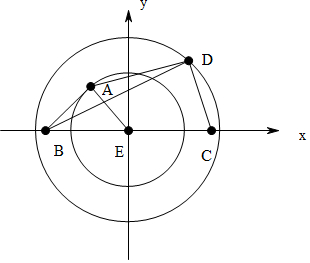 解:以E为原点,以BC为x轴建立平面直角坐标系,
解:以E为原点,以BC为x轴建立平面直角坐标系,
∵EA=1,ED=$\sqrt{3}$,
∴A在以E为圆心,以1为半径的圆上,D在以E为圆心,以$\sqrt{3}$为半径的圆上,
设A(cosθ,sinθ),B(-a,0),C(a,0),D($\sqrt{3}$cosα,$\sqrt{3}$sinα),
则$\overrightarrow{AB}$=(-a-cosθ,-sinθ),
$\overrightarrow{AC}$=(a-cosθ,-sinθ),
$\overrightarrow{BD}$=($\sqrt{3}$cosα+a,$\sqrt{3}$sinα),
$\overrightarrow{DC}$=(a-$\sqrt{3}$cosα,-$\sqrt{3}$sinα),
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=cos2θ-a2+sin2θ=1-a2=-1,∴a2=2,
∴$\overrightarrow{BD}$•$\overrightarrow{DC}$=a2-3cos2α-3sin2α=2-3=-1.
故答案:-1
点评 本题考查了平面向量的数量积运算,建立坐标系,将向量运算转化为坐标运算是关键,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.在下列向量组中,可以把向量$\overrightarrow{a}$=(3,-2)表示出来的是( )
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,2) | B. | $\overrightarrow{{e}_{1}}$=(-1,2),$\overrightarrow{{e}_{2}}$=(5,-2) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=(-2,3) |
20.下列推理中属于归纳推理且结论正确的是( )
| A. | 由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n | |
| B. | 由f(x)=xcosx满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数 | |
| C. | 由圆x2+y2=r2的面积S=πr2,推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab | |
| D. | 由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
17.函数y=3x-4x3(x∈[0,2])的最大值是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
14.已知函数f(x)=(2x-x2)ex,给以下四个结论:①f(x)>0的解集为{x|0<x<2};②$f({-\sqrt{2}})$是极小值,$f({\sqrt{2}})$是极大值;③f(x)有极小值,但无最小值;④f(x)有极小值,也有最小值.其中正确的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②④ |
18.函数f(x)=($\frac{1}{2}$)x-log2x的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |