题目内容
在等比数列{an}中，a3+a8=-31，a4a7=-32，公比q是整数，则a10= ．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由等比数列的性质和韦达定理可得a3和a8为方程x2+31x-32=0的两根，解方程易得a3和a8，可得公比q，由通项公式可得．
解答：
解：∵在等比数列{an}中，a3+a8=-31，a4a7=-32，
∴由等比数列的性质可得a3a8=a4a7=-32，
∴a3和a8为方程x2+31x-32=0的两根，
解方程可得
，或
又∵公比q是整数，∴
，∴q=-2
∴a10=a8q2=-32×4=-128
故答案为：-128
∴由等比数列的性质可得a3a8=a4a7=-32，
∴a3和a8为方程x2+31x-32=0的两根，
解方程可得
|
|
又∵公比q是整数，∴
|
∴a10=a8q2=-32×4=-128
故答案为：-128
点评：本题考查等比数列的通项公式和性质，涉及韦达定理，属基础题．
练习册系列答案
相关题目
已知sinα cosα=
，则sinα+cosα=（ ）
| 1 |
| 2 |
| A、2 | ||
| B、0 | ||
C、
| ||
D、±
|
若全集U=Z，集合A={n|
∈z}，集合B={n|
∈z}，则A∩{CuB}是（ ）
| n |
| 2 |
| n |
| 3 |
| A、{n|n=3k+1，k∈z} |
| B、{n|n=4k或n=4k+2，k∈z} |
| C、{n|n=6k±1，k∈z} |
| D、{n|n=6k±2，k∈z} |
若关于x的方程
x2+
x-
b+3=0与
x2+
x-a+6=0在R上都有解，则23a•2b 的最小值为（ ）
| 1 |
| 2 |
| 2a |
| 1 |
| 2 |
| 1 |
| 4 |
| 2b |
| A、256 | B、128 |
| C、64 | D、32 |
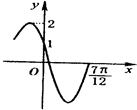
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
，若|f（x）|≥2m，则m的取值范围是（ ）
|
| A、[-2，0] |
| B、（-∞，0] |
| C、[-2，1] |
| D、[-1，0] |