题目内容
5．一动圆圆心在抛物线x2=4y上．该圆过点（0，1）．且与定直线l相切，则直线l的方程为y=-1．分析 根据抛物线方程可求得其焦点坐标，要使圆过点（0，1）且与定直线l相切，需圆心到定点的距离与定直线的距离相等，根据抛物线的定义可知，定直线正是抛物线的准线，进而根据抛物线方程求得准线方程即可．
解答 解：根据抛物线方程可知抛物线焦点为（0，1），
∴定点为抛物线的焦点，
要使圆过点（0，1）且与定直线l相切，需圆心到定点的距离与定直线的距离相等，
根据抛物线的定义可知，定直线正是抛物线的准线，
其方程为y=-1．
故答案为y=-1．
点评 本题主要考查了抛物线的定义．对涉及过抛物线焦点的直线的问题时常借助抛物线的定义来解决．
练习册系列答案
相关题目
15．
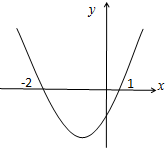若函数f（x）在R上可导，其导函数为f′（x），且函数y=（1-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）
若函数f（x）在R上可导，其导函数为f′（x），且函数y=（1-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A． | 函数f（x）有极大值f（-2），无极小值 | B． | 函数f（x）有极大值f（1），无极小值 | ||
| C． | 函数f（x）有极大值f（-2）和极小值f（1） | D． | 函数f（x）有极大值f（1）和极小值f（-2）． |
16．已知圆（x-1）2+（y-1）2=4上到直线y=x+b的距离等于1的点有且仅有2个，则b的取值范围是（ ）
| A． | （-$\sqrt{2}$，0）U（0，$\sqrt{2}$） | B． | （-3$\sqrt{2}$，3$\sqrt{2}$） | C． | （-3$\sqrt{2}$，-$\sqrt{2}$）U（$\sqrt{2}$，3$\sqrt{2}$） | D． | （-3$\sqrt{2}$，-$\sqrt{2}$]U（$\sqrt{2}$，3$\sqrt{2}$） |
13．若正数x，y满足4x+y-1=0，则$\frac{x+y}{xy}$的最小值为（ ）
| A． | 12 | B． | 10 | C． | 9 | D． | 8 |