若x＞2.求$\frac{{x}^{2}-4x+5}{x-2}$的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

15．若x＞2，求$\frac{{x}^{2}-4x+5}{x-2}$的最小值．

分析 $\frac{{x}^{2}-4x+5}{x-2}$=（x-2）+$\frac{1}{x-2}$，当x＞2时，x-2＞0，由基本不等式，可得其最小值．

解答解：$\frac{{x}^{2}-4x+5}{x-2}$=（x-2）+$\frac{1}{x-2}$，
当x＞2时，x-2＞0，
故（x-2）+$\frac{1}{x-2}$≥2$\sqrt{（x-2）•\frac{1}{x-2}}$=2，
故当x＞2时，$\frac{{x}^{2}-4x+5}{x-2}$的最小值为2．

点评本题考查的知识点是函数的最值及其几何意义，基本不等式的应用，难度中档．

练习册系列答案

6．已知f（x）是定义域为R的函数，且满足f（x+2）=-$\frac{1}{f（x）}$，当2≤x≤3时，f（x）=x+$\frac{1}{2}$，则f（-$\frac{11}{2}$）=3．

3．

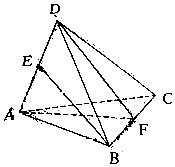如图，在空间四边形ABCD中，AB，BC，CD，DA的长和两条对角线AC，BD都相等，且E为AD的中点，F为BC的中点，则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$．

10．用0，1，2，3，4，5这6个数字可以组成多少个没有重复的4位数？其中有多少个是2的倍数？

20．在四面体S-ABC中，AB⊥BC，AB=BC=$\sqrt{2}$，SA=SC=2，SB=$\sqrt{6}$，则该四面体外接球的体积是（　　）

7．已知函数$f（x）=\sqrt{3+2x-{x^2}}$的定义域为A，集合B={x|x²-2mx+m²-9≤0}．
（1）若A∩B=[2，3]，求实数m的值；
（2）若?x₁∈A，?x₂∈（C_RB），使x₂=x₁，求实数m的取值范围．

15．已知函数f（x）=3sinωxcosωx-$\sqrt{3}$cos²ωx+2sin²（ωx-$\frac{π}{12}$）+$\frac{{\sqrt{3}}}{2}$，（ω＞0）的最小正周期为π．
（1）求f（x）的递增区间．
（2）在△ABC中，角A，B，C的对边分别为a，b，c，已知a=1，b=$\sqrt{2}$，f（A）=1，求∠C的大小．

16．已知圆x²+y²=16的圆心为P，点Q（a，b）在圆P外，以PQ为直径作圆M与圆P相交于A，B两点．
（1）试确定直线QA，QB与圆P的位置关系，若QA=QB=3，写出点Q所在曲线的方程；
（2）若a=4，b=6，求直线AB的方程．

试题分类