题目内容
10.若x,y满足$\left\{{\begin{array}{l}{x+2y≤2}\\{x+y≥0}\\{x≤4}\end{array}}\right.$,则z=2x+3y的取值范围是[-4,5].分析 画出不等式组表示的可行域,由z=2x+3y的几何意义:z表示直线在y轴上纵截距3倍,平移直线即可得到取值范围.
解答  解:作出x,y满足$\left\{{\begin{array}{l}{x+2y≤2}\\{x+y≥0}\\{x≤4}\end{array}}\right.$的可行域,
解:作出x,y满足$\left\{{\begin{array}{l}{x+2y≤2}\\{x+y≥0}\\{x≤4}\end{array}}\right.$的可行域,
z=2x+3y的几何意义:z表示直线在y轴上纵截距3倍,
画出直线2x+3y=0,平移可得直线通过A(4,-1)时,
z取得最大值8-3=5;
直线通过B(4,-4)时,z取得最小值8-12=-4.
则z=2x+3y的取值范围是[-4,5].
故答案为:[-4,5].
点评 本题考查线性规划的简单运用:求最值,注意运用可行域,运用平移直线法,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
20.若直线x+y-1=0与抛物线y=2x2交于A,B两点,则点M(1,0)到A,B两点的距离之积为( )
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
18.在△ABC中,根据下列条件解三角形,则其中有两个解的是( )
| A. | a=80,b=61,A=60° | B. | a=10,b=14,A=30° | ||
| C. | b=23,A=45°,B=30° | D. | a=61,c=47,A=120° |
15.已知f(x)为R上的可导函数,且对x∈R,均有f(x)>f′(x),则有( )
| A. | e2016f(-2016)<f(0),f(2016)<e2016f(0) | B. | e2016f(-2016)>f(0),f(2016)>e2016f(0) | ||
| C. | e2016f(-2016)<f(0),f(2016)>e2016f(0) | D. | e2016f(-2016)>f(0),f(2016)<e2016f(0) |
2.已知集合p={x|y=lg(x-1)},Q={y|y=2-|x|},R为实数集,则( )
| A. | p?Q | B. | P∩Q=∅ | C. | P∪Q=Q | D. | CRP=Q |
20.在四面体S-ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,SA=SC=2,SB=$\sqrt{6}$,则该四面体外接球的体积是( )
| A. | 8$\sqrt{6}$π | B. | $\sqrt{6}$π | C. | 24π | D. | 6π |
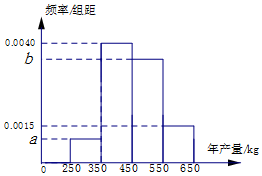 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.