题目内容
若圆的一条直径的两个端点分别是(-1,3)和(5,-5),则此圆的方程是( )
| A、x2+y2+4x+2y-20=0 |
| B、x2+y2-4x-2y-20=0 |
| C、x2+y2-4x+2y+20=0 |
| D、x2+y2-4x+2y-20=0 |
考点:圆的一般方程
专题:计算题,直线与圆
分析:由已知的两点为直径的两端点,可得连接两点的线段的中点为圆心,连接两点线段长度的一半为圆的半径,故由中点坐标公式求出两点的中点,即为圆心坐标,利用两点间的距离公式求出两点间的距离,求出距离的一半即为圆的半径,根据求出的圆心坐标和半径写出圆的方程即可.
解答:
解:∵(-1,3)和(5,-5)为一条直径的两个端点,
∴两点的中点(2,-1)为圆的圆心,
又两点间的距离d=
=10,
∴圆的半径为5,
则所求圆的方程为(x-2)2+(y+1)2=25,即x2+y2-4x+y-20=0.
故选D
∴两点的中点(2,-1)为圆的圆心,
又两点间的距离d=
| 36+64 |
∴圆的半径为5,
则所求圆的方程为(x-2)2+(y+1)2=25,即x2+y2-4x+y-20=0.
故选D
点评:此题考查了圆的标准方程,涉及的知识有:中点坐标公式,两点间的距离公式,以及圆标准方程与一般式方程的转化,其中根据题意求出圆心坐标和圆的半径是解本题的关键.

练习册系列答案
相关题目
已知焦点在y轴上的椭圆
+
=1的长轴长为8,则m等于( )
| x2 |
| 10 |
| y2 |
| m |
| A、4 | B、8 | C、10 | D、16 |
已知直线y=k(x+1)与抛物线C:y2=4x相交于A、B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、
|
已知向量
=(2sinA,cosA),
=(cosA,2
cosA),
•
=
,若A∈[0,
],则A=( )
| a |
| b |
| 3 |
| a |
| b |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=cos(ωx+
)(x∈R,ω>0)的最小正周期为π,为了得到f(x)的图象,只需将函数g(x)=sin(ωx+
)的图象( )
| π |
| 3 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
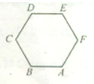
如图,正六边形ABCDEF中,
+
+
=( )
| BA |
| CD |
| BC |

A、
| ||
B、
| ||
C、
| ||
D、
|
(文做)设
<(
)b<(
)a<1,那么( )
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| A、aa<bb<ba |
| B、aa<bb<a |
| C、ab<ba<aa |
| D、ab<aa<ba |