题目内容
在△ABC中，内角A，B，C依次成等差数列，AB=8，BC=5，则△ABC外接圆的面积为（ ）
A、
| ||
| B、16π | ||
C、
| ||
| D、15π |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题设条件，先求出角B，再由余弦定理求出AC，然后利用正弦定理求出∴△ABC外接圆半径，由此能求出△ABC外接圆面积．
解答：
解：∵△ABC中，内角A，B，C依次成等差数列，
∴A+C=2B，
∴A+B+C=3B=180°，解得B=60°，
∵AB=8，BC=5，
∴AC2=82+52-2×8×5×cos60°=49，
∴AC=7，
∴△ABC外接圆半径R=
×
=
，
∴△ABC外接圆面积S=π•(
)2=
．
故选：A．
∴A+C=2B，
∴A+B+C=3B=180°，解得B=60°，
∵AB=8，BC=5，
∴AC2=82+52-2×8×5×cos60°=49，
∴AC=7，
∴△ABC外接圆半径R=
| 1 |
| 2 |
| 7 |
| sin60° |
7
| ||
| 3 |
∴△ABC外接圆面积S=π•(
7
| ||
| 3 |
| 49π |
| 3 |
故选：A．
点评：本题考查三角形外接圆面积的求法，是中档题，解题时要注意等差数列、正弦定理、余弦定理等知识点的合理运用．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
下列各式中，求导运算正确的是（ ）
| A、（uv）′=u′v′ | ||||
B、（
| ||||
| C、（uv）′=uv+u′v′ | ||||
D、（
|
如图程序，输出的结果A是（ ）
| A、5 | B、6 | C、15 | D、120 |
已知向量
=（1，2），
=（x，-6），若
∥
，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、-3 | B、3 | C、12 | D、-12 |
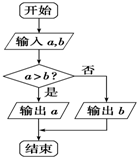如图所示的程序框图，其功能是（ ）| A、输入a，b的值，按从小到大的顺序输出它们的值 |
| B、输入a，b的值，按从大到小的顺序输出它们的值 |
| C、求a，b的最大值 |
| D、求a，b的最小值 |
已知集合A={x|y=lg[x（x-2）]}，B={x|
＜1}，则A∩B等于（ ）
| 1 |
| x |
| A、（-∞，0）∪（2，+∞） |
| B、（2，+∞） |
| C、（1，2） |
| D、（-∞，0）∪（1，2） |
数列0.9，0.99，0.999，0.9999，…的一个通项公式是（ ）
A、an=1-
| ||
B、an=1-
| ||
C、an=1-
| ||
D、an=1-
|
若函数f（x）可导，则f′（x0）等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|