题目内容
在平面直角坐标系xOy中,若动点P(a,b)到两直线l1:y=x和l2:y=-x+2的距离之和为
,则a2+b2的最大值为 .
| 2 |
考点:点到直线的距离公式
专题:直线与圆
分析:由已恬得l1,l2交点为T(1,1),l1⊥l2,P在l1,l2的右侧时,过P分别向l1,l2引垂线,垂足分别为Q,R,那么|PQ|+|PR|=
过P做y轴的平行线,与l1,l2交点为C,B,则|PQ|=|TR|,|PR|=|RB|,点P轨迹为正方形ABCD,由此能求出a2+b2=|PO|2的最大值.
| 2 |
解答:
解:若动点P(a,b)到两直线l1:y=x和l2:y=-x+2的距离之和为
, l1,l2交点为T(1,1),l1,l2的斜率分别为-1,1,则l1⊥l2,
l1,l2交点为T(1,1),l1,l2的斜率分别为-1,1,则l1⊥l2,
P在l1,l2的右侧时,过P分别向l1,l2引垂线,
垂足分别为Q,R,那么|PQ|+|PR|=
过P做y轴的平行线,
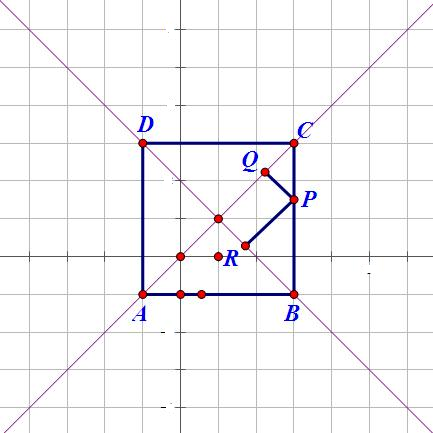
与l1,l2交点为C,B如图,
则|PQ|=|TR|,|PR|=|RB|
∴|TR|+|RB|=
,
其它位置同理,那么点P轨迹为正方形ABCD,
当P在C(2,2)时,
|PO|取得最大值2
,即a2+b2=|PO|2取得最大值8.
故答案为:8.
| 2 |
 l1,l2交点为T(1,1),l1,l2的斜率分别为-1,1,则l1⊥l2,
l1,l2交点为T(1,1),l1,l2的斜率分别为-1,1,则l1⊥l2,P在l1,l2的右侧时,过P分别向l1,l2引垂线,
垂足分别为Q,R,那么|PQ|+|PR|=
| 2 |
过P做y轴的平行线,
与l1,l2交点为C,B如图,
则|PQ|=|TR|,|PR|=|RB|
∴|TR|+|RB|=
| 2 |
其它位置同理,那么点P轨迹为正方形ABCD,
当P在C(2,2)时,
|PO|取得最大值2
| 2 |
故答案为:8.
点评:本题考查代数和的最大值的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
函数y=ax-2的零点有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
已知f(x)的定义域为{x|x∈R,x≠1}且f(x)的图象关于(1,0)对称,当x<1时,f(x)=2x2-x+1,则当x>1时,f(x)的减区间为( )
A、[
| ||
B、[
| ||
C、(1,
| ||
D、(1,
|
 函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|< 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断: