题目内容
5．如图，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示GH，MN是异面直线的图形的序号为（ ）
| A． | ①② | B． | ③④ | C． | ①③ | D． | ②④ |
分析 判定异面直线的方法：①根据它的判定定理：“经过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线．”②定义法：不在同一个平面内的．两条直线称为异面直线；③反证法：既不平行又不相交的直线即为异面直线．
解答 解：异面直线的判定定理：“经过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线．”
根据异面直线的判定定理可知：在图②④中，直线GH、MN是异面直线；
在图①中，由G、M均为棱的中点可知：GH∥MN；
在图③中，∵G、M均为棱的中点，∴四边形GMNH为梯形，则GH与MN相交．
故选D．
点评 本题主要考查了空间中直线与直线之间的位置关系，考查空间想象能力和思维能力．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
15．一个几何体的三视图如图所示，则该几何体的表面积为（ ）
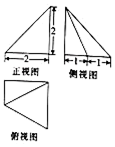
| A． | $12+\sqrt{3}$ | B． | $10+\sqrt{3}$ | C． | $10+2\sqrt{3}$ | D． | $11+\sqrt{3}$ |
13．已知复数z1=2-i，z2=1+i，其中i为虚数单位，设复数z=$\frac{{z}_{1}}{{z}_{2}}$，若a-z为纯虚数，则实数a的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{3}{2}$ | D． | -$\frac{1}{2}$ |
20．已知复数z=$\frac{2i}{1+i}$，复数z对应的点为Z，O为坐标原点，则向量$\overrightarrow{OZ}$的坐标为（ ）
| A． | （-1，-1） | B． | （1，-1） | C． | （-1，1） | D． | （1，1） |
10．设A、B、C为锐角△ABC的三个内角，M=sinA+sinB+sinC，N=cosA+2cosB，则（ ）
| A． | M＜N | B． | M=N | C． | M＞N | D． | M、N大小不确定 |
17．
某手机生产企业为了解消费者对某款手机功能的认同情况，通过销售部随机抽取50名购买该款手机的消费者，并发出问卷调查，该问卷只有30份给予回复，这30份的评分如下：
（Ⅰ）完成茎叶图，并求16名男消费者评分的中位数与14名女消费者评分的平均值；
（Ⅱ）若大于40分为“满意”，否则为“不满意”，完成上面的2×2列联表，并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关．
参考公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
参考数据：
某手机生产企业为了解消费者对某款手机功能的认同情况，通过销售部随机抽取50名购买该款手机的消费者，并发出问卷调查，该问卷只有30份给予回复，这30份的评分如下：| 男 | 47，36，28，48，29，48，44，50，46，46，42，45，50，37，35，49 |
| 女 | 38，35，37，48，47，36，38，45，39，29，49，28，44，33 |
（Ⅱ）若大于40分为“满意”，否则为“不满意”，完成上面的2×2列联表，并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关．
| 满意 | 不满意 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
参考数据：
| P（K2≥k0） | 0.05 | 0.025 | 0.01 |
| k0 | 3.841 | 5.024 | 6.635 |
14．设a=（$\frac{7}{9}$）${\;}^{-\frac{1}{4}}$，b=（$\frac{9}{7}$）${\;}^{\frac{1}{5}}$，c=log2$\frac{9}{7}$，则a，b，c的大小顺序是（ ）
| A． | b＜a＜c | B． | c＜a＜b | C． | c＜b＜a | D． | b＜c＜a |
15．已知一个球的表面上有A、B、C三点，且AB=AC=BC=2$\sqrt{3}$，若球心到平面ABC的距离为1，则该球的表面积为（ ）
| A． | 20π | B． | 15π | C． | 10π | D． | 2π |