题目内容
 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.(1)求证:BD1∥平面A1DE;
(2)求:DE与面A1D1B成角余弦值;
(3)在线段AB上是否存在点M,使二面角D1-MC-D的大小为
| π |
| 4 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,直线与平面所成的角
专题:空间角
分析:(1)连结AD1,交A1D于点O,由EO为△ABD1的中位线,能证明BD1∥平面A1DE.
(2)以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出DE与面A1D1B成角余弦值.
(3)设在线段AB上是否存在点M,使二面角D1-MC-D的大小为
,设M(1,y0,0),(0≤y0≤2),求出平面D1MC的法向量,利用向量法能求出AM的长是2-
.
(2)以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出DE与面A1D1B成角余弦值.
(3)设在线段AB上是否存在点M,使二面角D1-MC-D的大小为
| π |
| 4 |
| 3 |
解答:
(1)证明:连结AD1,交A1D于点O,
∵四边形ADD1A1为正方形,
∴O是AD1的中点,∵点E为AB的中点,连接OE.
∴EO为△ABD1的中位线,∴EO∥BD1,
又∵BD1不包含于平面A1DE,OE?平面A1DE,
∴BD1∥平面A1DE.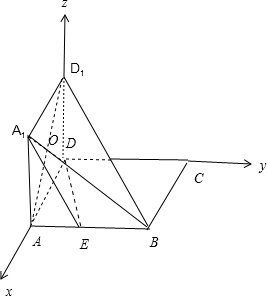
(2)解:由题意可得:D1D⊥平面ABCD,以点D为原点,
DA,DC,DD1所在直线分别为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,
∵正方形AA1D1D与矩形ABCD所在平面互相垂直,
AB=2AD=2,点E为AB的中点,
∴D(0,0,0),E(1,1,0),B(1,2,0),
A1(1,0,1),D1(0,0,1),
∴
=(1,1,0),
=(0,-2,1),
=(-1,-2,1),
设平面A1B1D的法向量
=(x,y,z),
则
,
取y=1,得
=(0,1,2),
设直线DE与面A1D1B所成的角为θ,
则sinθ=|cos<
,
>|=|
|=
.
∴cosθ=
=
.
∴DE与面A1D1B成角余弦值为
.
(3)解:设在线段AB上是否存在点M,使二面角D1-MC-D的大小为
,
设M(1,y0,0),(0≤y0≤2),
∵D1(0,0,1),C(0,2,0),
∴
=(1,y0-2,0),
=(0,-2,1),
设平面D1MC的法向量为
=(x1,y1,z1),
则
,
取x1=2-y0,得
=(2-y0,1,2),
∵平面ECD的一个法向量为
=(0,0,1),
∵二面角D1-EC-D的大小为
,
∴cos<
,
>=
=
,
解y0=2-
,∴M(1,2-
,0),A(1,0,0),
∴|
|=2-
,
故线段AB上是存在点M(1,2-
,0),
使二面角D1-MC-D的大小为
,AM的长是2-
.
∵四边形ADD1A1为正方形,
∴O是AD1的中点,∵点E为AB的中点,连接OE.
∴EO为△ABD1的中位线,∴EO∥BD1,
又∵BD1不包含于平面A1DE,OE?平面A1DE,
∴BD1∥平面A1DE.

(2)解:由题意可得:D1D⊥平面ABCD,以点D为原点,
DA,DC,DD1所在直线分别为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,
∵正方形AA1D1D与矩形ABCD所在平面互相垂直,
AB=2AD=2,点E为AB的中点,
∴D(0,0,0),E(1,1,0),B(1,2,0),
A1(1,0,1),D1(0,0,1),
∴
| DE |
| BA1 |
| BD1 |
设平面A1B1D的法向量
| m |
则
|
取y=1,得
| m |
设直线DE与面A1D1B所成的角为θ,
则sinθ=|cos<
| DE |
| m |
| 1 | ||||
|
| ||
| 10 |
∴cosθ=
1-
|
3
| ||
| 10 |
∴DE与面A1D1B成角余弦值为
3
| ||
| 10 |
(3)解:设在线段AB上是否存在点M,使二面角D1-MC-D的大小为
| π |
| 4 |
设M(1,y0,0),(0≤y0≤2),
∵D1(0,0,1),C(0,2,0),
∴
| CM |
| CD1 |
设平面D1MC的法向量为
| n |
则
|
取x1=2-y0,得
| n |
∵平面ECD的一个法向量为
| p |
∵二面角D1-EC-D的大小为
| π |
| 4 |
∴cos<
| n |
| p |
| 2 | ||
|
| ||
| 2 |
解y0=2-
| 3 |
| 3 |
∴|
| AM |
| 3 |
故线段AB上是存在点M(1,2-
| 3 |
使二面角D1-MC-D的大小为
| π |
| 4 |
| 3 |
点评:本题考查的知识点是直线与平面平行的证明,用空间向量求平面间的夹角,空间中直线与直线之间的位置关系,直线与平面平行的判定,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题正确的是( )
A、y=sin(2x+
| ||||
| B、当φ<0时,y=sinx向右平移|φ|个单位可得y=sin(x-φ)的图象 | ||||
C、y=cosx的图象向左平移
| ||||
D、y=sinx的图象向左平移
|
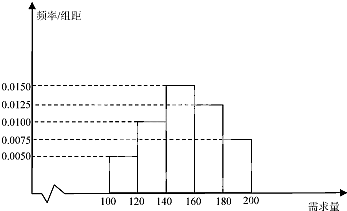 某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个丌学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个丌学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.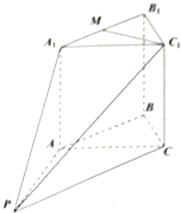 如图所示,在正三棱柱(底面是正三角形的直棱柱)A1B1C1-ABC中,M为A1B1的中点,P∈平面ABC,PA⊥平面ACC1A1,且AB=AA1=4,PA=4
如图所示,在正三棱柱(底面是正三角形的直棱柱)A1B1C1-ABC中,M为A1B1的中点,P∈平面ABC,PA⊥平面ACC1A1,且AB=AA1=4,PA=4 如图,四棱锥P-ABCD的底面是边长为2的正方形,M是PC上一点,侧棱PA⊥底面ABCD,且PC与底面ABCD成45°角.
如图,四棱锥P-ABCD的底面是边长为2的正方形,M是PC上一点,侧棱PA⊥底面ABCD,且PC与底面ABCD成45°角.