题目内容
已知直线y=
与椭圆C:
+
=1(a>b>0)交于P、Q两点,F是C的右焦点,若|PQ|=2|FQ|,则C的离心率为 .
| b2 |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,y=
与
+
=1联立解得x=±C;从而写出|PQ|=2c,|FQ|=
;从而解得.
| b2 |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
解答:
解:由题意,y=
与
+
=1联立解得,
x=±C;
故|PQ|=2c,|FQ|=
;
则2c=2
;
即a2-c2-ac=0;
即1-e2-e=0;
解得e=
;
故答案为:
.
| b2 |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
x=±C;
故|PQ|=2c,|FQ|=
| b2 |
| a |
则2c=2
| b2 |
| a |
即a2-c2-ac=0;
即1-e2-e=0;
解得e=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了椭圆的性质应用,属于基础题.

练习册系列答案
相关题目
对于非空数集A,若实数M满足对任意的a∈A恒有a≤M,则M为A的上界;若A的所有上界中存在最小值,则称此最小值为A的上确界,那么下列函数的值域中具有上确界的是( )
A、y=
| ||||
B、y=(-
| ||||
C、y=
| ||||
| D、y=lnx |
若函数y1=2sinx(x∈[0,2π))在P处的切线平行于函数y2=2
(
+1)在Q处的切线,则直线PQ的斜率为( )
| x |
| x |
| 3 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
已知i为虚数单位,复数z1=3-ai,z2=1+2i,若
复平面内对应的点在第四象限,则实数a的取值范围为( )
| z1 |
| z2 |
| A、{a|a<-6} | ||
B、{a|-6<a<
| ||
C、{a|a<
| ||
D、{a|a<-6或a>
|
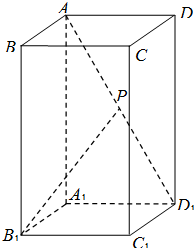 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).