题目内容
已知函数f（x）=x3-3x2-sinπx，则f（
）+f（
）+…+f（
）+f（
）=（ ）
| 1 |
| 2013 |
| 2 |
| 2013 |
| 4024 |
| 2013 |
| 4025 |
| 2013 |
| A、4025 | B、-4025 |
| C、8050 | D、-8050 |
考点：函数的值
专题：函数的性质及应用
分析：由已知条件得f（
）+f（
）+…+f（
）+f（
）=
-3×
=4025×
=-8050．
| 1 |
| 2013 |
| 2 |
| 2013 |
| 4024 |
| 2013 |
| 4025 |
| 2013 |
| 13+23+…+40253 |
| 20133 |
| 12+22+…+40252 |
| 20132 |
| -4026 |
| 2013 |
解答：
解：∵f（x）=x3-3x2-sinπx，
∴f（
）+f（
）+…+f（
）+f（
）
=[（
）3-3（
）2-sin（
）]+[（
）3-3（
）2-sin（
）]
+…+[（
）3-3（
）2-sin（
）]
=
-3×
=
-3×
=
-
=
=4025×
=-8050．
故选：D．
∴f（
| 1 |
| 2013 |
| 2 |
| 2013 |
| 4024 |
| 2013 |
| 4025 |
| 2013 |
=[（
| 1 |
| 2013 |
| 1 |
| 2013 |
| π |
| 2013 |
| 2 |
| 2013 |
| 1 |
| 2013 |
| 2π |
| 2013 |
+…+[（
| 4025 |
| 2013 |
| 4025 |
| 2013 |
| 4025π |
| 2013 |
=
| 13+23+…+40253 |
| 20133 |
| 12+22+…+40252 |
| 20132 |
=
[
| ||
| 20133 |
| ||
| 20132 |
=
| 40252•20132 |
| 20133 |
| 4025•2013•8051 |
| 20132 |
=
| 4025(4025-8051) |
| 2013 |
=4025×
| -4026 |
| 2013 |
=-8050．
故选：D．
点评：本题考查函数值的求法，是中档题，解题时要注意数列的性质的灵活运用．
练习册系列答案
相关题目
如图，若输入n的值为4，则输出m的值为（ ）
| A、-3 | ||
B、
| ||
| C、2 | ||
D、-
|
将y=f（x）的图象向右平移一个单位长度，所得图象与y=lnx关于y轴对称，则y=f（x）的解析式为（ ）
| A、f（x）=ln（x+1） |
| B、f（x）=ln（x-1） |
| C、f（x）=ln（-x+1） |
| D、f（x）=ln（-x-1） |
已知a=20.6，b=log0.62，c=0.62，则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，当x＞0时，f（x）=
则函数g（x）=4f（x）-1的零点个数为（ ）
|
| A、4 | B、6 | C、8 | D、10 |
设函数f（x）=tanx-2x+π（-
＜x＜
，且x≠kπ+
，k∈Z），则f（x）的所有零点之和为（ ）
| 2013π |
| 2 |
| 2015π |
| 2 |
| π |
| 2 |
| A、1007π |
| B、1008π |
| C、2014π |
| D、2016π |
集合{x|-4＜x-1＜4，x∈N，且x≠0}的真子集的个数是（ ）
| A、32 | B、31 | C、16 | D、15 |
已知函数f（x）是R上的增函数，A（0，-1），B（3，1）是其图象上的两点，那|f（x）|＜1的解集是（ ）
| A、（-∞，-1]∪[3，+∞） |
| B、（0，3） |
| C、（-3，0） |
| D、（-∞，0]∪[1，+∞） |
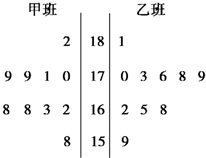随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．