题目内容
设集合A={(x,y)|(x-1)2+y2≤25},B={(x,y)|(x+1)2+y2≤25},C={(x,y)||x|≤t,|y|≤t,t>0},当C⊆(A∩B)时,t的取值范围为 .
考点:集合的包含关系判断及应用
专题:阅读型
分析:根据三个集合的形式得到集合A表示的是以(1,0)为圆心,以5为半径的圆的内部,B表示的是以(-1,0)为圆心,以5为半径的圆的内部,C表示由直线x=±t,y=±t围成的正方形,将C⊆(A∩B)转化为正方形的顶点(t,t)不在圆(x+1)2+y2=25的外部即可
解答:
解:∵(x-1)2+y2=25表示以(1,0)为圆心,以5为半径的圆,
∴集合A={(x,y)|(x-1)2+y2≤25}表示的是以(1,0)为圆心,以5为半径的圆及其内部的点,
∵(x+1)2+y2=25表示的是以(-1,0)为圆心,以5为半径的圆,
∴B={(x,y)|(x+1)2+y2≤25}表示的是以(-1,0)为圆心,以5为半径的圆及其内部的点,
C={(x,y)||x|≤t,|y|≤t,t>0}表示由直线x=±t,y=±t围成的正方形,
∵C⊆(A∩B),
∴正方形的顶点(t,t)不在圆(x+1)2+y2=25的外部即可,
∴(t+1)2+t2≤25,
解得0<t≤3.
∴t的取值范围为(0,3].
∴集合A={(x,y)|(x-1)2+y2≤25}表示的是以(1,0)为圆心,以5为半径的圆及其内部的点,
∵(x+1)2+y2=25表示的是以(-1,0)为圆心,以5为半径的圆,
∴B={(x,y)|(x+1)2+y2≤25}表示的是以(-1,0)为圆心,以5为半径的圆及其内部的点,
C={(x,y)||x|≤t,|y|≤t,t>0}表示由直线x=±t,y=±t围成的正方形,
∵C⊆(A∩B),
∴正方形的顶点(t,t)不在圆(x+1)2+y2=25的外部即可,
∴(t+1)2+t2≤25,
解得0<t≤3.
∴t的取值范围为(0,3].
点评:本题考查集合包含关系的判定,圆的方程、直线的方程;将代数问题转化为几何问题来解决,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

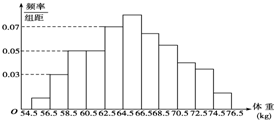 为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是
为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是