题目内容
14.在下列区间中,函数f(x)=lgx-$\frac{1}{x}$的零点所在的区间是( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 先求出f(2)f(3)<0,再由二分法进行判断.
解答 解:由于f(2)=lg2-$\frac{1}{2}$=lg2-lg$\sqrt{10}$<0,
f(3)=lg3-$\frac{1}{3}$=lg3-lg10${\;}^{\frac{1}{3}}$>0
∴f(2)f(3)<0,
根据二分法,得函数在区间(2,3)内存在零点.
故选:C
点评 本题考查函数的零点问题,解题时要注意二分法的合理运用.

练习册系列答案
相关题目
9.设集合A={x|-2≤x<2},集合B={x|-1<x<3},那么A∪B=( )
| A. | {x|-2≤x<3} | B. | {-1,0,1} | C. | {x|-1<x<2} | D. | {0,1,2} |
6.已知点M(x,y)满足$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0\end{array}\right.$,若ax+y的最大值为1,则a的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ y≥x-1\\ x+y≤4\end{array}\right.$,目标函数z=x+y,则当z=3时,x2+y2的取值范围是( )
| A. | $[\frac{{3\sqrt{2}}}{2},\sqrt{5}]$ | B. | $[\frac{{3\sqrt{2}}}{2},5]$ | C. | $[\frac{9}{2},5]$ | D. | $[\sqrt{5},\frac{9}{2}]$ |
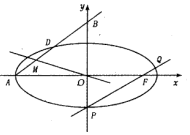 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.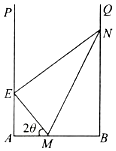 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.