题目内容
2.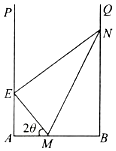 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
分析 (1)设∠AME=2θ,求出EM,MN,即可求用θ表示的l函数表达式,并写出定义域;
(2)令f(θ)=sinθ(1-sinθ),sinθ∈(0,$\frac{\sqrt{2}}{2}$),即可求l的最小值.
解答 解:(1)∵EM=BM,∠B=∠MEN,
∴△BMN≌△EMN,
∴∠BNM=∠MNE,
∵∠AME=2θ,
∴∠BNM=∠MNE=θ,
设MN=x,
在△BMN中,BM=xsinθ,∴EM=BM=xsinθ,
∴△EAM中,AM=EMcos2θ=xsinθcos2θ,
∵AM+BM=a,
∴xsinθcos2θ+xsinθ=a,
∴x=$\frac{a}{sinθcos2θ+sinθ}$,
∴l=EM+MN=$\frac{a}{2sinθ(1-sinθ)}$,θ∈(0,$\frac{π}{4}$);
(2)令f(θ)=sinθ(1-sinθ),sinθ∈(0,$\frac{\sqrt{2}}{2}$),
∴f(θ)≤$\frac{1}{4}$,
当且仅当θ=$\frac{π}{6}$时,取得最大值$\frac{1}{4}$,此时lmin=2a.
点评 本题考查利用数学知识解决实际问题,考查三角函数模型的运用,属于中档题.

练习册系列答案
相关题目
12.在△ABC中,a,b,c分别是A,B,C的对边,$a=2\sqrt{3},b=2\sqrt{2}$,且1+2cos(B+C)=0,则BC边上的高等于( )
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
13.实数x,y满足$\left\{\begin{array}{l}x≤3\\ x+y≥0\\ x-y+6≥0.\end{array}\right.$若z=ax+y的最大值为3a+9,最小值为3a-3,则a的取值范围是( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |
7.某小区停车场的收费标准为:每车每次停车时间不超过2小时免费,超过2小时的部分每小时收费1元(不足1小时的部分按1小时计算).现有甲乙两人独立来停车场停车(各停车一次),且两人停车时间均不超过5小时.设甲、乙两人停车时间(小时)与取车概率如表所示.
(1)求甲、乙两人所付车费相同的概率;
(2)设甲、乙两人所付停车费之和为随机变量ξ,求ξ的分布列和数学期望Eξ.
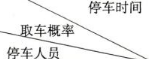 | (0,2] | (2,3] | (3,4] | (4,5] |
| 甲 | $\frac{1}{2}$ | x | x | x |
| 乙 | $\frac{1}{6}$ | $\frac{1}{3}$ | y | 0 |
(2)设甲、乙两人所付停车费之和为随机变量ξ,求ξ的分布列和数学期望Eξ.
14.在下列区间中,函数f(x)=lgx-$\frac{1}{x}$的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
 如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.
如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.