题目内容
20.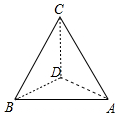 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.
分析 根据方位角求出∠ADB,利用仰角的正切值得出AD,BD关系,在△ABD中使用余弦定理解出AD,BD,从而得出CD.
解答 解:作出平面ABD的方位图如图所示
由题意可知∠WAD=20°,∠EAD=40°,设∠ABE=θ,则∠WAB=θ,
∴∠DBA+∠DAB=40°-θ+20°+θ=60°,∴∠ABD=120°,
设BD=x,AD=y,则由余弦定理得AB2=x2+y2-2xycos∠ADB,
即16900=x2+y2+xy.
在Rt△BCD中,∵tan∠CBD=$\frac{CD}{BD}=\frac{CD}{x}=\frac{\sqrt{3}}{3}$,∴CD=$\frac{\sqrt{3}x}{3}$,
在Rt△ACD中,∵tan∠CAD=$\frac{CD}{AD}=\frac{CD}{y}=\sqrt{3}$,∴CD=$\sqrt{3}y$.
∴x=3y.
解方程组$\left\{\begin{array}{l}{16900={x}^{2}+{y}^{2}+xy}\\{x=3y}\end{array}\right.$得$\left\{\begin{array}{l}{x=30\sqrt{13}}\\{y=10\sqrt{13}}\end{array}\right.$.
∴CD=$\sqrt{3}y$=10$\sqrt{39}$.
故答案为:10$\sqrt{39}$.
点评 本题考查了解三角形的实际应用,求出∠ADB及AD,BD的关系是解题关键.

练习册系列答案
相关题目
11.如图所示的程序运行后输出的结果是( )


| A. | -5 | B. | -3 | C. | 0 | D. | 1 |
5.函数y=$\frac{x}{\sqrt{lo{g}_{\frac{1}{2}}(4x-3)}}$的定义域为( )
| A. | ($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,1] | D. | ($\frac{3}{4}$,1) |
9. 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
(Ⅰ)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过4000元的居民中随机抽出2户进行捐款援助,设抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,根据表格中所给数据,分别求b,c,a+b,c+d,a+c,b+d,a+b+c+d的值,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表参考公式:,${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:(Ⅰ)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过4000元的居民中随机抽出2户进行捐款援助,设抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,根据表格中所给数据,分别求b,c,a+b,c+d,a+c,b+d,a+b+c+d的值,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | a=30 | b | |
| 捐款不超 过500元 | c | d=6 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |