题目内容
15．已知实数x，y满足$\left\{\begin{array}{l}x-y+2≤0\\ x+y-4≤0\\ x+2y-4≥0\end{array}\right.$，则y-2x的最小值为1．分析 画出约束条件表示的可行域，利用目标函数的几何意义，求出最小值即可．
解答 
解：根据方程组获得可行域如下图，令z=y-2x，可化为y=2x+z，
因此，当直线过点（1，3）时，z取得最小值为1．
故答案为：1．
点评 本题主要考查线性规划问题，是一道常规题．从二元一次方程组到可行域，再结合目标函数的几何意义，全面地进行考查．
练习册系列答案
名校课堂系列答案
相关题目
11．A，B，C是△ABC的三个内角，若$\overrightarrow{m}$=（sin2$\frac{B+C}{2}$，1），$\overrightarrow{n}$=（-2，cos2A+1），且$\overrightarrow{m}$⊥$\overrightarrow{n}$，则cosA=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$或1 | D． | $\frac{1}{2}$或0 |
6．小明、小王、小张、小李4名同学排成一纵队表演节目，其中小明不站排头，小张不站排尾，则不同的排法共有（ ）种．
| A． | 14 | B． | 18 | C． | 12 | D． | 16 |
10．
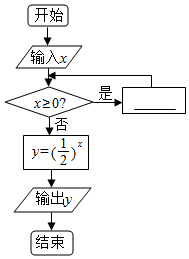已知①x=x-1，②x=x-2，③x=x-3，④x=x-4在如图所示的程序框图中，如果输入x=10，而输出y=4，则在空白处可填入（ ）
已知①x=x-1，②x=x-2，③x=x-3，④x=x-4在如图所示的程序框图中，如果输入x=10，而输出y=4，则在空白处可填入（ ）| A． | ①②③ | B． | ②③ | C． | ③④ | D． | ②③④ |
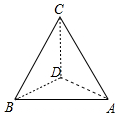如图，为了估测某塔的高度，在同一水平面的A，B两点处进行测量，在点A处测得塔顶C在西偏北20°的方向上，仰角为60°；在点B处测得塔顶C在东偏北40°的方向上，仰角为30°．若A，B两点相距130m，则塔的高度CD=10$\sqrt{39}$ m．
