题目内容
9．
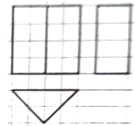如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为32π．
分析 由已知可得该几何体是一个以俯视图为底面的三棱柱，求出底面外接圆半径r及球心到底面的距离d，结合棱柱的外接球半径R满足：R2=r2+d2和球的表面积公式，可得答案．
解答 解：由已知可得该几何体是一个以俯视图为底面的三棱柱，
底面为直角三角形，故底面外接圆半径r=2，
棱柱的高为4，故球心到底面的距离d=2，
故棱柱的外接球半径R满足：R2=r2+d2=8，
故棱柱的外接球表面积S=4πR2=32π，
故答案为：32π
点评 本题考查的知识点球内接多面体，球的体积与表面积公式，难度中档．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
19．设F1、F2是双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两个焦点，P是C1上一点，若|PF1|+|PF2|=6a，且△PF1F2最小内角的大小为30°，抛物线C2：y2=12x的准线交双曲线C1所得的弦长为4$\sqrt{3}$，则双曲线C1的实轴长为（ ）
| A． | 6 | B． | 2$\sqrt{6}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
20．阅读如图的程序框图，运行相应的程序，则输出的值为（ ）
| A． | 81 | B． | 27 | C． | 16 | D． | 9 |
4．
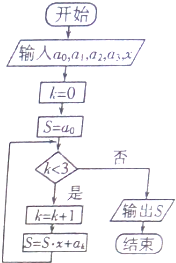如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法，执行该程序框图，则输出的结果S表示的值为（ ）
如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法，执行该程序框图，则输出的结果S表示的值为（ ）| A． | a0+a1+a2+a3 | B． | （a0+a1+a2+a3）x3 | ||
| C． | a0+a1x+a2x2+a3x3 | D． | a0x3+a1x2+a2x+a3 |
14．若函数f（x）=$\left\{\begin{array}{l}{{a}^{x}，x＜0}\\{（a-3）x+4a，x≥0}\end{array}\right.$（a＞0，且a≠1）的值域为（-∞，+∞），则实数a的取值范围是（ ）
| A． | （3，+∞） | B． | （0，$\frac{1}{4}$] | C． | （1，3） | D． | [$\frac{1}{4}$，1） |