题目内容
10.已知函数f(x)=x3+$\sqrt{{a}^{2}{x}^{2}-ax+\frac{1}{4}}$(a≥0).(1)当a=1时,求函数f(x)的单调区间;
(2)求证:函数f(x)有且只有一个零点.
分析 (1)a代入可得f(x)=x3+|x-$\frac{1}{2}$|,分区间讨论去绝对值得出函数的单调区间;
(2)整理得f(x)=x3+|ax-$\frac{1}{2}$|,构造函数令h(x)=-x3,g(x)=|ax-$\frac{1}{2}$|,函数零点问题相当于两函数交点问题,通过数形结合,得出结论.
解答  解:(1)当a=1时,
解:(1)当a=1时,
f(x)=x3+|x-$\frac{1}{2}$|,
当x≥$\frac{1}{2}$时,f(x)=x3+x-$\frac{1}{2}$|,显然递增;
当x<$\frac{1}{2}$时,f(x)=x3-x+$\frac{1}{2}$|,
f'(x)=3x2-1,
∴当x∈(-∞,-$\frac{\sqrt{3}}{3}$)时,f'(x)>0,函数递增,
当x∈(-$\frac{\sqrt{3}}{3}$,$\frac{1}{2}$)时,f'(x)<0,函数递减,
(2)f(x)=x3+|ax-$\frac{1}{2}$|,
令h(x)=-x3,g(x)=|ax-$\frac{1}{2}$|,
画出函数h(x)图象如图:
由g(x)=|ax-$\frac{1}{2}$|图象可知有且只有一个交代,
∴函数f(x)有且只有一个零点.
点评 本题考查了分段函数单调性问题和利用构造函数的方法解决函数零点问题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
20.i是虚数单位,复数z=$\frac{2}{1+i}$+2-3i,则|z|=( )
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
18.已知cos2($\frac{x}{2}$+$\frac{π}{4}$)=cos(x+$\frac{π}{6}$),则cosx等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
5.如图所示的框图,若输入的n的值为4,则输出的S=( )
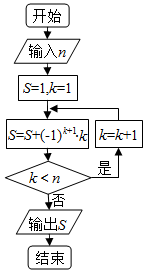

| A. | 3 | B. | 4 | C. | -1 | D. | 0 |
15.某地市高三理科学生有15000名,在一次调研测试中,数学成绩ξ服从正态分布N(100,σ2),已知p(80<ξ≤100)=0.35,若按成绩分层抽样的方式取100份试卷进行分析,则应从120分以上的试卷中抽取( )
| A. | 5份 | B. | 10份 | C. | 15份 | D. | 20份 |
19.已知命题p:?x∈R,x2+2x+3=0,则¬p是( )
| A. | ?x∈R,x2+2x+3≠0 | B. | ?x∈R,x2+2x+3=0 | C. | ?x∈R,x2+2x+3≠0 | D. | ?x∈R,x2+2x+3=0 |
20.为了解从事微商的人的年龄分布情况,某调查机构所辖市的A,B两个街区中随机抽取了50名微商的年龄进行了调查统计,结果如表:
已知从50名微商中随机抽取一名,抽到年龄在30~40的概率为0.3.
(1)求x,y的值,根据表中数计算两个街区年龄在30岁以下从事微商的概率;
(2)为了解这50名微商的工作生活情况,决定按表中描述的六种情况进行分层抽样,从中选取10名作为一个样本进行跟踪采访,然后再从样本中年龄在25~30的人员中随机选取2人接受电视台专访,求接受专访的2人来自不同街区的概率.
| 年龄段(岁) | 20~25 | 25~30 | 30~40 |
| A街区 | 5 | x | 10 |
| B街区 | 5 | 10 | y |
(1)求x,y的值,根据表中数计算两个街区年龄在30岁以下从事微商的概率;
(2)为了解这50名微商的工作生活情况,决定按表中描述的六种情况进行分层抽样,从中选取10名作为一个样本进行跟踪采访,然后再从样本中年龄在25~30的人员中随机选取2人接受电视台专访,求接受专访的2人来自不同街区的概率.