题目内容
10.过点A(4,$\frac{3π}{2}$)引圆ρ=4sinθ的一条切线,则切线长为( )| A. | 3$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 把极坐标转化为直角坐标,利用ρ2=x2+y2,ρsinθ=y,极坐标方程转化为直角坐标方程,利用勾股定理求出切线长.
解答 解:∵在极坐标系中,过点A(4,$\frac{3π}{2}$)引圆ρ=4sinθ的一条切线,
在直角坐标系下,A(0,-4),
方程化为x2+y2-4y=0,
如图:圆心(0,2),半径:2
切线长为:$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$.
故选:D.
点评 本题考查点的极坐标和直角坐标的互化,考查转化思想,计算能力,是基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
15.A,B,C为圆O上三点,且直线OC与直线AB交于圆外一点,若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,则m+n的范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
20.设函数f'(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f'(x)-3,则6f(x)>f'(x)的解集为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | (e,+∞) | D. | $(\frac{e}{3},+∞)$ |
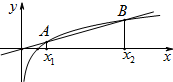 如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)
如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)