题目内容
19．函数f（x）=4$\sqrt{x}$+$\sqrt{x（x-1）}$的定义域为{x|x=0或x≥1}．分析 由根式内部的代数式大于等于0联立不等式组求解．
解答 解：由$\left\{\begin{array}{l}{x≥0}\\{x（x-1）≥0}\end{array}\right.$，得x=0或x≥1．
∴函数f（x）=4$\sqrt{x}$+$\sqrt{x（x-1）}$的定义域为：{x|x=0或x≥1}．
故答案为：{x|x=0或x≥1}．
点评 本题考查函数的定义域及其求法，考查了不等式组的解法，是基础题．
练习册系列答案
相关题目
10．过点A（4，$\frac{3π}{2}$）引圆ρ=4sinθ的一条切线，则切线长为（ ）
| A． | 3$\sqrt{3}$ | B． | 6$\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 4$\sqrt{2}$ |
7．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别F1（-c，0），F2（c，0），若椭圆上存在点P，使得csin∠PF1F2=asin∠PF2F1≠0，则离心率e的取值范围是（ ）
| A． | $（0，\frac{{\sqrt{2}}}{2}）$ | B． | $（\sqrt{2}-1，1）$ | C． | $[\sqrt{2}-1，1）$ | D． | $（0，\sqrt{2}-1]$ |
14．已知双曲线的中心为原点，离心率e=$\sqrt{5}$，且它的一个焦点与抛物线x2=-8$\sqrt{5}$y的焦点重合，则此双曲线方程为（ ）
| A． | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B． | $\frac{y^2}{4}-\frac{x^2}{16}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{16}=1$ |
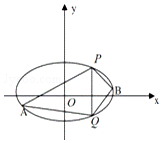已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，椭圆C的一个短轴端点与抛物线x2=4y的焦点重合．
9．已知a，b，c满足4a=9，b=log${\;}_{\frac{1}{3}}$5，c3=$\frac{3}{5}$，则（ ）
| A． | a＜b＜c | B． | b＜c＜a | C． | c＜a＜b | D． | c＜b＜a |