题目内容
20.设函数f'(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f'(x)-3,则6f(x)>f'(x)的解集为( )| A. | (0,+∞) | B. | (1,+∞) | C. | (e,+∞) | D. | $(\frac{e}{3},+∞)$ |
分析 容易求出f′(0)=6,结合条件便可得出函数f(x)的解析式,进而求出导函数,代入6f(x)>f′(x),根据指数函数的单调性便可解出原不等式.
解答 解:根据条件,f(0)=1,且3f(x)=f'(x)-3,
可得3f(0)=3=f′(0)-3;
∴f′(0)=6,
由于ex的导数为ex,且由复合函数的导数法则,
可设f(x)=menx+b,可得3menx+3b=mnenx-3,
显然3b=-3,即b=-1;又3m=mn,即n=3,
由f(0)=m-1=1,即m=2,
∴f(x)=2e3x-1,f′(x)=6e3x;
∴由6f(x)>f′(x)得:6(2e3x-1)>6e3x,
整理得,e3x>1,
∴3x>0,
∴x>0.
∴原不等式的解集为(0,+∞).
故选:A.
点评 本题考查导函数的概念,基本初等函数和复合函数的求导,指数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.过点A(4,$\frac{3π}{2}$)引圆ρ=4sinθ的一条切线,则切线长为( )
| A. | 3$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
15.已知f(x)为R上的可导函数,且对x∈R,均有f(x)>f′(x),则有( )
| A. | e2016f(-2016)<f(0),f(2016)<e2016f(0) | B. | e2016f(-2016)>f(0),f(2016)>e2016f(0) | ||
| C. | e2016f(-2016)<f(0),f(2016)>e2016f(0) | D. | e2016f(-2016)>f(0),f(2016)<e2016f(0) |
12.在△ABC中,a,b,c为角A,B,C的对边,若b=1,c=$\sqrt{3}$,A=$\frac{π}{6}$,则cos5B=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-1 | D. | -$\frac{\sqrt{3}}{2}$或0 |
9.已知a,b,c满足4a=9,b=log${\;}_{\frac{1}{3}}$5,c3=$\frac{3}{5}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
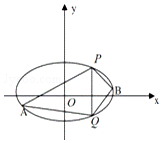 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.