题目内容

如图，已知正方形ABCD是圆M：（x-4）2+（y-4）2=4的内接正方形，AB，AD的中点分别是E，F，当正方形ABCD绕圆心M转动，同时点F在边AD上运动时则
ME
•
OF
的取值范围是（　　）
A、[-8
2
，8
2
]
B、[-8，8]
C、[-4
2
，4
2
]
D、[-4，4]
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于M点坐标能确定，所以OM就能确定，这样就可把
OF
表示成
OM
+
MF
，这样就不难求出
ME
•
OF
的范围了．
解答： 解：由题意得：
OF
=
OM
+
MF
，∴
ME
•
OF
=
ME
•(
OM
+
MF
)=
ME
•
OM
+
ME
•
MF
；
∵ME⊥MF，∴
ME
•
MF
=0；
∴
ME
•
OF
=
ME
•
OM
；
由题意得：圆M的半径为2，故ME=
2
；又OM=4
2
；
∴
ME
•
OM
=8cos＜
ME
，
OM
＞，即
ME
•
OF
=8cos＜
ME
，
OM
＞；
所以-8≤
ME
，
OM
＞≤8，
故选：B．
点评：本题的关键就是得出
OF
=
OM
+
MF
，根据数量积的运算和余弦函数的取值便不难得出答案．
练习册系列答案
相关题目
当-
π
2
≤x≤
π
2
时，函数f（x）=sinx+
3
cosx的值域为
 
．
等比数列{an}的前n项和为Sn，若S9是S3与S6的等差中项，则公比q的值为（　　）
A、1或
-
34
2
B、
-
34
2
C、1
D、-1或
34
2
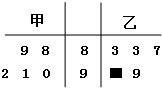如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩，期中一个数字被污损，则甲的平均成绩不超过乙的平均成绩的概率为（　　）
A、
4
5
B、
3
5
C、
2
5
D、
1
5
由曲线y2=x与y=x，y=
3
所围成图形的面积是（　　）
A、S=
∫
3
0
（y-y2）dy
B、S=
∫
3
1
（x-
x
）dx
C、S=
∫
1
0
（y2-y）dx
D、S=
∫
3
1
（y2-y）dy
下列函数中值域为（0，+∞）的是（　　）
A、y=
1
2-x
B、y=（
1
3
）1-x
C、y=
(
1
2
)x-1
D、y=
1-2x
已知双曲线
x2
a2
-y2=1（a＞0）的实轴长为2，则该双曲线的离心率为（　　）
A、
2
2
B、
5
2
C、
5
D、
2
若双曲线x2-
y2
b2
=1（b＞0）的一条渐近线与圆x2+（y-2）2=1至多有一个交点，则双曲线离心率的取值范围是（　　）
A、（1，2]
B、[2，+∞）
C、（1，
3
]
D、[
3
，+∞）
若执行如图所示的程序框图，当输入n=1，m=5，则输出p的值为（　　）
A、-4B、1C、2D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网