题目内容
5.已知向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,则|$\overrightarrow{a}-\overrightarrow{b}$|的取值范围为( )| A. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | B. | ($\sqrt{7}$-1,$\sqrt{7}$+1) | C. | [1,2] | D. | (1,2) |
分析 利用向量的数量积运算性质和模的计算公式及不等式的性质即可得出
解答 解:∵向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,如图
∴设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,则$\overrightarrow{CA}=\overrightarrow{a}-\overrightarrow{c}$,$\overrightarrow{CB}=\overrightarrow{b}-\overrightarrow{c}$,所以CA⊥CB,如图,OA=OB=2,取AB中点D,设CD=x,则AB=2x,
则OD⊥AB,AO2=DO2+AD2,所以DO=$\sqrt{4-{x}^{2}}$,根据CD-CO≤OD≤CO+CD,
∴1-x$≤\sqrt{4-{x}^{2}}≤$1+x,解得$\frac{\sqrt{7}-1}{2}≤x≤\frac{\sqrt{7}+1}{2}$,
∴$\overrightarrow{a}-\overrightarrow{b}$=2x∈[$\sqrt{7}-1,\sqrt{7}+1$].
故选A.
点评 本题考查了向量的运算;借助于三角形法则等是解答的关键;要熟练掌握数量积运算性质、模的计算公式.

| A. | 1.6 | B. | 3.2 | C. | 6.4 | D. | 12.8 |
| A. | {x|x≤1} | B. | {1,2} | C. | {-1,0,1 } | D. | R |
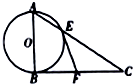 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.