题目内容
5.若集合A={x|x≥0},且A∩B=B,则集合B可能是( )| A. | {x|x≤1} | B. | {1,2} | C. | {-1,0,1 } | D. | R |
分析 由已知可得B⊆A,然后逐一核对四个选项得答案.
解答 解:∵A∩B=B,∴B⊆A,
又A={x|x≥0},可知B满足,
故选:B.
点评 本题考查交集及其运算,关键是由已知得到集合A与B的关系,是基础题.

练习册系列答案
相关题目
20.已知点F为抛物线y=-$\frac{1}{8}{({x-4})^2}$的焦点,E为抛物线的顶点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PE|的最小值为( )
| A. | 6 | B. | $2+4\sqrt{2}$ | C. | $4+2\sqrt{5}$ | D. | $2\sqrt{13}$ |
5.已知向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,则|$\overrightarrow{a}-\overrightarrow{b}$|的取值范围为( )
| A. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | B. | ($\sqrt{7}$-1,$\sqrt{7}$+1) | C. | [1,2] | D. | (1,2) |
12.掷两枚均匀的骰子,已知点数不同,则至少有一个是3点的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
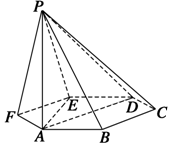 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.