��Ŀ����
1����ֱ������ϵ��ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵȡ��ͬ�ĵ�λ���ȣ���ֱ֪��I�IJ�������Ϊ$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$��tΪ��������ԲC�ļ����귽��Ϊ��=2����P���ڼ���ԳƵĵ�P'QUOTE p?�ļ�����Ϊ$��\sqrt{2}��\frac{5��}{4}��$��1��д��ԲC��ֱ�����귽�̼���P�ļ����ꣻ��2����ֱ��I��ԲC�ཻ������A��B�����P��A��B����ľ���֮����
���� ��1�����ü�������ֱ������Ļ�������д��ԲC��ֱ�����귽�̣����õ�P���ڼ���ԳƵĵ�P'�ļ�����Ϊ$��\sqrt{2}��\frac{5��}{4}��$���õ���P�ļ����ꣻ
��2����ֱ��I��ԲC�ཻ������A��B����$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$����x2+y2=4���ã�$|{t_1}{t_2}|=\frac{1}{2}$���������P��A��B����ľ���֮����
��� �⣺��1��ԲC�ļ����귽��Ϊ��=2��ֱ�����귽��Ϊx2+y2=4��
��P���ڼ���ԳƵĵ�P'�ļ�����Ϊ$��\sqrt{2}��\frac{5��}{4}��$����P��$\sqrt{2}��\frac{��}{4}$����
��2����P��Ϊֱ������ΪP��1��1��
��$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$����x2+y2=4���ã�$|{t_1}{t_2}|=\frac{1}{2}$��
���ԣ���P��A��B����ľ���֮��$\frac{1}{2}$��
���� ���⿼�鼫������ֱ������Ļ���������������̵����ã���������ļ������壬�����е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
12�����⡰?x0��∁RQ��x03��Q���ķ��ǣ�������
| A�� | ?x0∉∁RQ��x03��Q | B�� | ?x0��∁RQ��x03��Q | C�� | ?x∉∁RQ��x3��Q | D�� | ?x��∁RQ��x3∉Q |
5����֪����$\overrightarrow{a}��\overrightarrow{b}��\overrightarrow{c}$����|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2��|$\overrightarrow{c}$|=1����$\overrightarrow{a}-\overrightarrow{c}$��•��$\overrightarrow{b}-\overrightarrow{c}$��=0����|$\overrightarrow{a}-\overrightarrow{b}$|��ȡֵ��ΧΪ��������
| A�� | [$\sqrt{7}$-1��$\sqrt{7}$+1] | B�� | ��$\sqrt{7}$-1��$\sqrt{7}$+1�� | C�� | [1��2] | D�� | ��1��2�� |
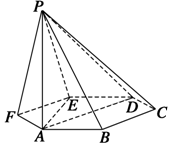 ��ͼ����֪����P-ABCDEF�ĵ������������Σ�PA��ƽ��ABC��PA=2AB�������н�����ȷ������Ǣܣ�
��ͼ����֪����P-ABCDEF�ĵ������������Σ�PA��ƽ��ABC��PA=2AB�������н�����ȷ������Ǣܣ�