题目内容
13.画出函数y=$\frac{{x}^{2}}{{2}^{x}-1}$的大致图象.分析 确定函数的定义域,函数值的趋向,即可得出结论.
解答  解:由题意,函数的定义域为(-∞,0)∪(0,+∞),当x趋向于正无穷时,函数的值趋向于0,当x趋向于负无穷时,函数的值趋向于负无穷,
解:由题意,函数的定义域为(-∞,0)∪(0,+∞),当x趋向于正无穷时,函数的值趋向于0,当x趋向于负无穷时,函数的值趋向于负无穷,
如图所示.
点评 本题主要考查了指数函数和幂函数的图象和性质,属于基础题.

练习册系列答案
相关题目
3.非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\sqrt{3}$|$\overrightarrow{a}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$-$\overrightarrow{a}$夹角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
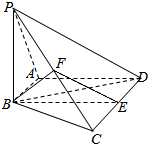 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.