题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a+b)cosC+ccosB=0(Ⅰ)求角C的大小.
(Ⅱ)若c=6,求△ABC面积的最大值.
分析 (Ⅰ)利用正弦定理将(2a+b)cosC+ccosB=0化简,可得角C的大小.c=6,利用余弦定理,构造基本不等式,即可求解△ABC面积的最大值.
解答 解:(Ⅰ)根据(2a+b)cosC+ccosB=0,由正弦定理可得:2sinAcosC+sinBcosC+sinCcosB=0.
即2sinAcosC=-sinA,
∵0<A<π,sinA≠0,
∴cosC=-$\frac{1}{2}$
∵0<C<π
∴C=$\frac{2π}{3}$.
(Ⅱ)∵c=6,C=$\frac{2π}{3}$.
由余弦定理:可得${c}^{2}={a}^{2}+{b}^{2}-2abcos\frac{2π}{3}$
即36=a2+b2+ab,
∵a2+b2≥2ab(当且仅当a=b时取等号)
∴3ab≤36,即ab≤12.
故得△ABC面积S=$\frac{1}{2}$absinC$≤\frac{1}{2}×12×\frac{\sqrt{3}}{2}=3\sqrt{3}$.
即△ABC面积的最大值为$3\sqrt{3}$.
点评 本题主要考查了正弦定理,余弦定理的化简计算能力,和基本不等式求最值的运用.属于基础题.

练习册系列答案
相关题目
11.下列选项中说法正确的是( )
| A. | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B. | 向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}>0$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C. | 若am2≤bm2,则a≤b | |
| D. | “?x0∈R,x02-x0≤0”的否定是“?x∈R,x2-x≥0” |
12.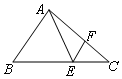 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
16.在直三棱柱ABC-A1BlC1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
6.随着教育制度和高考考试制度的改革,高校选拔人才的方式越来越多.某高校向一基地 学校投放了一个保送生名额,先由该基地学校初选出10名优秀学生,然后参与高校设置的 考核,考核设置了难度不同的甲、乙两个方案,每个方案都有M(文化)、N(面试)两个考核内 容,最终选择考核成绩总分第一名的同学定为该高校在基地校的保送生.假设每位同学完成 每个方案中的M、N两个考核内容的得分是相互独立的.根据考核前的估计,某同学完成甲 方案和乙方案的M、N两个考核内容的情况如表:
表1:甲方案
表2:乙方案
已知该同学最后一个参与考核,之前的9位同学的最高得分为125分.
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
表1:甲方案
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
13.宿州市日前提出,要提升市民的生活质量,改善民生,促进“中国梦”的实线,为此,某记者在街头随机采访了100名市民,根据他们对“中国梦”实线的信心情况进行统计分析,得到如下分布表:
(Ⅰ)以这100名市民信心指数为样本来估计市民的总体信心指数,若要从全市市民中随机任选3人进行信心跟踪,记ξ表示抽到信心级别为“非常有信心或有信心”市民人数,求ξ的分布列及期望;
(Ⅱ)从这100名市民中,任选两人,记他们的信心指数分别为m、n,求|m-n|≥60的概率.
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数(分数) | 90 | 60 | 30 | 6 |
| 人数(名) | 42 | 38 | 14 | 6 |
(Ⅱ)从这100名市民中,任选两人,记他们的信心指数分别为m、n,求|m-n|≥60的概率.
10.已知函数$f(x)=\frac{1}{3}m{x^3}+\frac{1}{2}n{x^2}+x+2017$,其中m∈{2,4,6,8},n∈{1,3,5,7},从这些函数中任取不同的两个函数,在它们在(1,f(1))处的切线相互平行的概率是( )
| A. | $\frac{7}{120}$ | B. | $\frac{7}{60}$ | C. | $\frac{7}{30}$ | D. | 以上都不对 |