题目内容
已知函数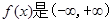 上的奇函数,且
上的奇函数,且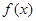 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当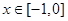 时,
时,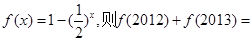 .
.
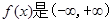 上的奇函数,且
上的奇函数,且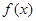 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当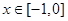 时,
时,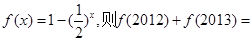 .
.1
试题分析:因为
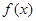 的图象关于直线x=1对称,所以
的图象关于直线x=1对称,所以 ,
,所以
 ,又
,又 ,所以
,所以 
所以
 ,所以
,所以 ,故
,故 .
.所以


点评:解决本题的关键是从对称性入手,逐步代换得出函数的周期,从而达到求值的目的.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
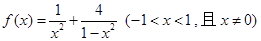 .
.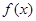 的最小值;
的最小值;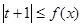 恒成立,求实数
恒成立,求实数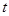 的取值范围.
的取值范围.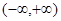 上的单调性,并用定义证明.
上的单调性,并用定义证明.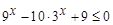 ,求函数
,求函数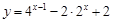 的最大值和最小值;
的最大值和最小值;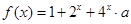 在
在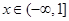 上f (x)
上f (x)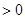 恒成立,求a的取值范围.
恒成立,求a的取值范围.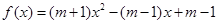
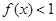 的解集为
的解集为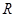 ,求
,求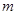 的取值范围;
的取值范围;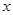 的不等式
的不等式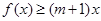 ;
;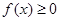 对一切
对一切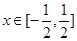 恒成立,求
恒成立,求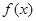 满足:对任意x∈R,都有
满足:对任意x∈R,都有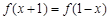 成立,且当
成立,且当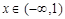 时,
时,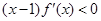 (其中
(其中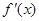 为
为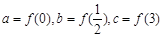 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )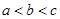
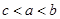
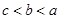
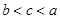
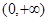 的函数
的函数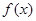 ,对任意的
,对任意的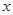 、
、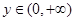 ,都有
,都有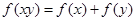 ,且当
,且当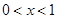 时,
时,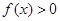 .
.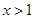 时,
时,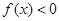 ;
;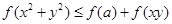 恒成立,求实数
恒成立,求实数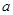 的取值范围.
的取值范围.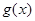 是
是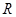 上的奇函数,且当
上的奇函数,且当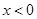 时
时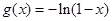 ,函数
,函数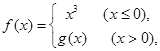 若
若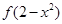 >
>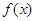 ,则实数
,则实数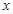 的取值范围是
的取值范围是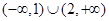
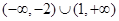

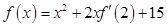 ,在闭区间
,在闭区间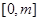 上有最大值15,最小值-1,则
上有最大值15,最小值-1,则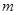 的取值范围是( )
的取值范围是( )