题目内容
已知定义在R上的函数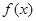 满足:对任意x∈R,都有
满足:对任意x∈R,都有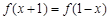 成立,且当
成立,且当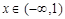 时,
时,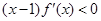 (其中
(其中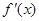 为
为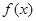 的导数).设
的导数).设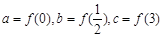 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )
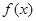 满足:对任意x∈R,都有
满足:对任意x∈R,都有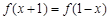 成立,且当
成立,且当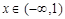 时,
时,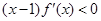 (其中
(其中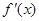 为
为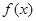 的导数).设
的导数).设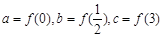 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )A.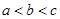 | B.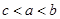 | C.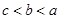 | D.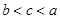 |
B
试题分析:由题意得:对任意x∈R,都有
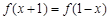 ,即f(x)=f(2-x)成立,
,即f(x)=f(2-x)成立,所以函数的对称轴为x=1,所以f(3)=f(-1).
因为当x∈(-∞,1)时,(x-1)f′(x)<0,
所以f′(x)>0,所以函数f(x)在(-∞,1)上单调递增.
因为-1<0<
 ,所以f(-1)<f(0)<f(
,所以f(-1)<f(0)<f( ),即f(3)<f(0)<f(
),即f(3)<f(0)<f( ),所以c<a<b.
),所以c<a<b.故选B.
点评:中档题,熟练掌握函数的性质如奇偶性、单调性、周期性、对称性等,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。自左向右看,函数图象上升,函数增;函数图象下降,函数减。

练习册系列答案
相关题目
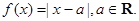
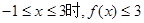 ,求
,求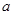 的取值范围;
的取值范围;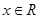 ,
,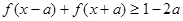 恒成立,求实数
恒成立,求实数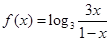 .
. 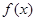 的图像关于点
的图像关于点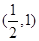 对称;
对称;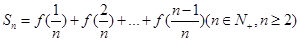 ,求
,求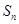 ;
;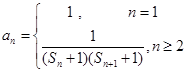
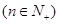 ,
,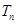 为数列
为数列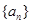 的前
的前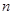 项和,若
项和,若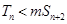 对一切
对一切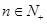 都成立,试求实数
都成立,试求实数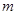 的取值范围.
的取值范围.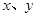 的二元一次方程组
的二元一次方程组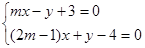 有唯一一组解,则实数
有唯一一组解,则实数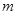 的取值范围是
的取值范围是 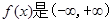 上的奇函数,且
上的奇函数,且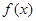 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当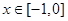 时,
时,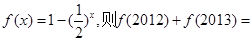 .
. ,
, 那么
那么 等于( )
等于( )



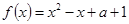
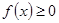 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。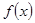 在区间
在区间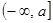 上的最小值
上的最小值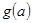 的表达式。
的表达式。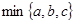 为
为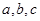 中的最小值,设
中的最小值,设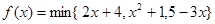 ,则
,则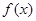 的最大值是 .
的最大值是 .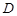 是函数
是函数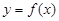 定义域内的一个区间,若存在
定义域内的一个区间,若存在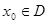 ,使
,使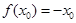 ,
,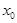 是
是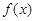 的一个“次不动点”,也称
的一个“次不动点”,也称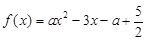 在区间
在区间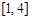 上存在次不动点,则实数
上存在次不动点,则实数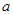 的取值范围
的取值范围