题目内容
已知函数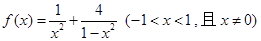 .
.
(Ⅰ)求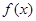 的最小值;
的最小值;
(Ⅱ)若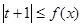 恒成立,求实数
恒成立,求实数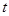 的取值范围.
的取值范围.
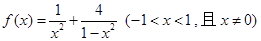 .
.(Ⅰ)求
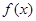 的最小值;
的最小值;(Ⅱ)若
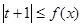 恒成立,求实数
恒成立,求实数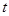 的取值范围.
的取值范围.(Ⅰ)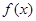 的最小值为
的最小值为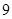 ;(Ⅱ)
;(Ⅱ)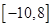 .
.
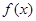 的最小值为
的最小值为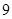 ;(Ⅱ)
;(Ⅱ)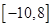 .
.试题分析:(Ⅰ)注意到分式中分母之间的关系
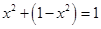 ,在分式上乘以
,在分式上乘以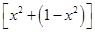 并展开,利用基本不等式可以求出函数
并展开,利用基本不等式可以求出函数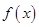 的最小值;(Ⅱ)在(Ⅰ)的基础上,将不等式
的最小值;(Ⅱ)在(Ⅰ)的基础上,将不等式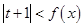 等价转化为
等价转化为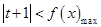 ,求出
,求出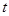 的取值范围即可.
的取值范围即可.试题解析:(Ⅰ)因为
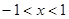 ,且
,且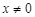 ,所以
,所以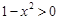 ,由柯西不等式
,由柯西不等式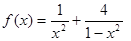
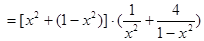
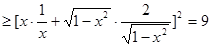 ,
,当且仅当
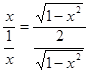 ,即
,即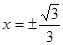 时取等号,
时取等号,∴
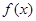 的最小值为
的最小值为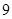 . 4分
. 4分(Ⅱ)由(Ⅰ)知
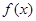 的最小值为
的最小值为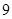 ,由题意可得
,由题意可得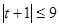 ,∴
,∴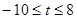 ,
,则实数
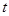 的取值范围为
的取值范围为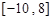 . 7分
. 7分
练习册系列答案
相关题目
 (x>0);②g(x)=x3;
(x>0);②g(x)=x3; )x;④φ()=lnx.
)x;④φ()=lnx.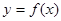 是增函数,且函数
是增函数,且函数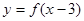 的图像关于(3,0)成中心对称,若
的图像关于(3,0)成中心对称,若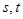 满足不等式
满足不等式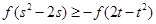 ,当
,当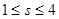 时,则
时,则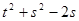 的取值范围为____.
的取值范围为____.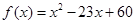 ,
,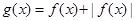 ,则
,则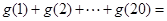 ( )
( )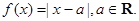
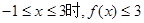 ,求
,求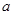 的取值范围;
的取值范围;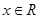 ,
,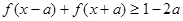 恒成立,求实数
恒成立,求实数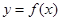 满足:
满足: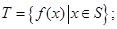 (ii)对任意
(ii)对任意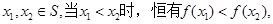
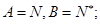
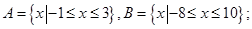
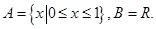
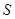 的最大允许值是多少?
的最大允许值是多少?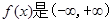 上的奇函数,且
上的奇函数,且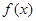 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当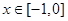 时,
时, .
.