题目内容
已知a是实数，函数f（x）=x2-2（a+2）x+a2．
（1）若关于x的方程f（x）=1有两个正根，求a的取值范围；
（2）若关于x的方程f（x）=1有两个都大于2的根，试求a的取值范围．
（1）若关于x的方程f（x）=1有两个正根，求a的取值范围；
（2）若关于x的方程f（x）=1有两个都大于2的根，试求a的取值范围．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：（1）关于x的方程即x2-2（a+2）x+a2-1=0，由题意可得△≥0，且x1+x2＞0，且且对称轴x=a+2＞0，且h（0）=a2-1＞0，由此求得a的范围．
（2）关于x的方程即g（x）=x2-2（a+2）x+a2-1=0，由题意可得△≥0，对称轴x=a+2＞2，g（2）=a2-4a-5＞0，由此求得a的范围．
（2）关于x的方程即g（x）=x2-2（a+2）x+a2-1=0，由题意可得△≥0，对称轴x=a+2＞2，g（2）=a2-4a-5＞0，由此求得a的范围．
解答：
解：（1）关于x的方程f（x）=1即x2-2（a+2）x+a2-1=0．
令h（x）=x2-2（a+2）x+a2-1，
由题意可得△=4（a+2）2-4（a2-1）≥0，且对称轴x=a+2＞0，且h（0）=a2-1＞0．
解得-
＜a＜-1，或 a＞1，
即a的范围是{a|-
＜a＜-1，或a＞1}．
（2）关于x的方程f（x）=1即x2-2（a+2）x+a2-1=0，
令g（x）=x2-2（a+2）x+a2-1，
由题意可得△=4（a+2）2-4（a2-1）≥0，对称轴x=a+2＞2，g（2）=a2-4a-5＞0，
解得 a≥5．
令h（x）=x2-2（a+2）x+a2-1，
由题意可得△=4（a+2）2-4（a2-1）≥0，且对称轴x=a+2＞0，且h（0）=a2-1＞0．
解得-
| 5 |
| 4 |
即a的范围是{a|-
| 5 |
| 4 |
（2）关于x的方程f（x）=1即x2-2（a+2）x+a2-1=0，
令g（x）=x2-2（a+2）x+a2-1，
由题意可得△=4（a+2）2-4（a2-1）≥0，对称轴x=a+2＞2，g（2）=a2-4a-5＞0，
解得 a≥5．
点评：本题主要考查了一元二次方程的根的分布与系数的关系，韦达定理，体现了转化的数学思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
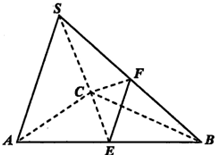在三棱锥S-ABC中，△ABC是边长为2的正三角形，平面SAC⊥平面ABC，
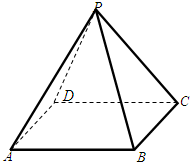在正四棱锥P-ABCD中，PA=2，直线PA与平面ABCD所成的角为60°．