题目内容
对于函数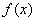 ,若存在
,若存在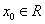 使得
使得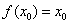 成立,则称
成立,则称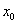 为
为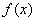 的不动点.
的不动点.
已知函数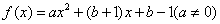 .
.
(1)若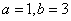 ,求函数
,求函数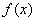 的不动点;
的不动点;
(2)若对任意实数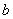 ,函数
,函数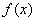 恒有两个相异的不动点,求
恒有两个相异的不动点,求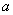 的取值范围;
的取值范围;
(3)在(2)的条件下,若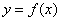 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数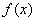 的不动点,且A、B两点关于直线
的不动点,且A、B两点关于直线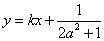 对称,求
对称,求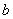 的最小值.
的最小值.
解:(1)若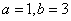 ,
, ,
, ,则
,则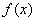 的不动点为
的不动点为
(2)函数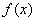 恒有两个相异的不动点,
恒有两个相异的不动点,
所以方程 即
即 恒有两个不等实根,
恒有两个不等实根,
需要判别式大于0恒成立,即 对任意实数
对任意实数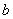 恒成立,
恒成立,
 ,所以
,所以 (3)因为A、B两点关于直线
(3)因为A、B两点关于直线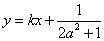 对称,所以
对称,所以 直线且中点
直线且中点 在直线上
在直线上
设 ,由(2)知,
,由(2)知,
所以 的中点
的中点
易知

由(2), 所以
所以
当且仅当

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 的二项展开式中,
的二项展开式中, 的系数为
的系数为  =(1,2),
=(1,2), =(1,0),
=(1,0), =(3,4).若λ为实数,(
=(3,4).若λ为实数,( 的大致图象是( )
的大致图象是( )

 ,
, ,
, ,全集为实数集
,全集为实数集 .
. ;
; ,求实数
,求实数 .
.  。
。 ,分别求
,分别求 和
和 的值; (7分)
的值; (7分) ,求
,求 的值。(7分)
的值。(7分)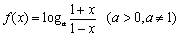
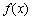 的定义域;
的定义域; 的
的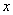 的取值范围.
的取值范围. 中,角
中,角 所对的对边长分别为
所对的对边长分别为 ;
; ,向量
,向量 ,向量
,向量 ,若
,若 ,求
,求 的值;
的值; ,且
,且 ,求
,求 .
.