题目内容
19．北纬45°圈上有A，B两地，A在东经120°，B在西经150°，设地球的半径为R，则A、B两地的球面距离是$\frac{πR}{3}$．分析 由于甲、乙两地在同一纬度圈上，计算经度差，求出甲、乙两地对应的AB弦长，以及球心角，然后求出球面距离．
解答 
解：地球表面上从甲地（北纬45°，东经120°）到乙地（北纬45°，西经150°）
甲、乙两地对应的AB的纬圆半径是$\frac{\sqrt{2}R}{2}$，经度差是90°，
所以AB=R
所以球心角是$\frac{π}{3}$，
所以甲、乙两地的球面距离是$\frac{πR}{3}$．
故答案为：$\frac{πR}{3}$．
点评 本题考查球面距离及其他计算，考查空间想象能力，是基础题．
练习册系列答案
相关题目
4．已知A、B是半径为R的球O的球面上两点，∠AOB=α，C为球面上的动点，若三棱锥O-ABC的体积最大，则α和最大体积分别为（ ）
| A． | $\frac{π}{3}$，$\frac{1}{6}$R3 | B． | $\frac{π}{3}$，$\frac{1}{3}$R3 | C． | $\frac{π}{2}$，$\frac{1}{3}$R3 | D． | $\frac{π}{2}$，$\frac{1}{6}$R3 |
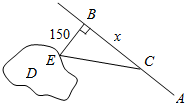如图，一海岛D，海岛离岸边最近点B的距离是150km，在岸边距点B300km的点A处有一批物资需运往海岛D，为了尽快送达海岛，A与B之间有一铁路，现用海陆联运的方式，火车的时速为50km，船的时速为30km，试在岸边选一点C，问选在何处可使运输时间最短．
17．下列函数中，满足“f（xy）=f（x）+f（y）”的单调递减函数是（ ）
| A． | f（x）=lnx | B． | f（x）=-x3 | C． | f（x）=log${\;}_{\frac{1}{2}}$x | D． | f（x）=3-x |