题目内容
16.已知以直线y=±kx(k>0)为渐近线的双曲线$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$(a>0,b>0)的离心率为e,且$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,则该双曲线的渐近线方程为( )| A. | $y=±\frac{\sqrt{2}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | y=$±\frac{1}{2}x$ |
分析 利用$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,可得$\frac{e}{k}$=$\sqrt{6}$,结合离心率公式,可得$\frac{\sqrt{1+\frac{1}{{k}^{2}}}}{k}$=$\sqrt{6}$,求出k,即可求出双曲线的渐近线方程.
解答 解:∵$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,
∴$\frac{e}{k}$=$\sqrt{6}$,
∴$\frac{\sqrt{1+\frac{1}{{k}^{2}}}}{k}$=$\sqrt{6}$,
∴k=$\frac{\sqrt{2}}{2}$,
∴该双曲线的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,
故选:A.
点评 本题考查双曲线的渐近线方程,考查学生的计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
4.已知A、B是半径为R的球O的球面上两点,∠AOB=α,C为球面上的动点,若三棱锥O-ABC的体积最大,则α和最大体积分别为( )
| A. | $\frac{π}{3}$,$\frac{1}{6}$R3 | B. | $\frac{π}{3}$,$\frac{1}{3}$R3 | C. | $\frac{π}{2}$,$\frac{1}{3}$R3 | D. | $\frac{π}{2}$,$\frac{1}{6}$R3 |
13.一几何体的三视图如图所示,则该几何体的表面积为( )
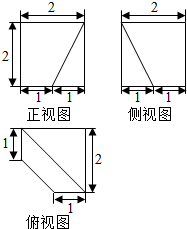

| A. | 20 | B. | 24 | C. | 16 | D. | $16+\frac{3}{2}\sqrt{10}$ |
14.设i为虚数单位,如果复数z满足(1-2i)z=5i,那么z的虚部为( )
| A. | -1 | B. | 1 | C. | i | D. | -i |
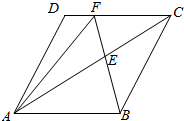 如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.
如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.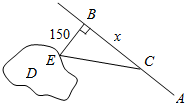 如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.
如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.