题目内容
已知一点A和平面a,求证:经过点A只能有一条直线和平面a垂直.
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:当点A在平面α内.假设经过点A至少有平面α的两条垂线,由此推导出在平面内经过A有两条垂线都和直线a垂直,这不成立;点A在平面α外,假设经过点A至少有平面α的两条垂线AB和AC,在平面内经过点A有两条直线都和BC垂直,也不成立.由此能证明经过一点A只能有平面α的一条垂线.
解答:
证明:根据点A和平面α的位置关系,分两种情况证明.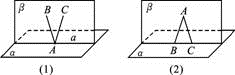 ①如图(1)所示,点A在平面α内.
①如图(1)所示,点A在平面α内.
假设经过点A至少有平面α的两条垂线AB、AC,
那么AB、AC是两条相交直线,
它们确定一个平面β,平面β和平面α相交于经过点A的一条直线a.
因为AB⊥平面α,AC⊥平面α,a?α,
所以AB⊥a,AC⊥a,在平面β内经过A有两条垂线都和直线a垂直,
这与平面几何中经过直线上一点只能有已知直线的一条垂线相矛盾.
②如图(2)所示,点A在平面α外,
假设经过点A至少有平面α的两条垂线AB和AC(B、C为垂足),
那么AB、AC是两条相交直线,它们确定一个平面β,
平面β和平面α相交于直线BC.
因为AB⊥平面α,AC⊥平面α,BC?α,所以AB⊥BC,AC⊥BC.
在平面β内经过点A有两条直线都和BC垂直,
与平面几何中经过直线外一点只能有已知直线的一条垂线相矛盾.
综上,经过一点A只能有平面α的一条垂线.
 ①如图(1)所示,点A在平面α内.
①如图(1)所示,点A在平面α内.假设经过点A至少有平面α的两条垂线AB、AC,
那么AB、AC是两条相交直线,
它们确定一个平面β,平面β和平面α相交于经过点A的一条直线a.
因为AB⊥平面α,AC⊥平面α,a?α,
所以AB⊥a,AC⊥a,在平面β内经过A有两条垂线都和直线a垂直,
这与平面几何中经过直线上一点只能有已知直线的一条垂线相矛盾.
②如图(2)所示,点A在平面α外,
假设经过点A至少有平面α的两条垂线AB和AC(B、C为垂足),
那么AB、AC是两条相交直线,它们确定一个平面β,
平面β和平面α相交于直线BC.
因为AB⊥平面α,AC⊥平面α,BC?α,所以AB⊥BC,AC⊥BC.
在平面β内经过点A有两条直线都和BC垂直,
与平面几何中经过直线外一点只能有已知直线的一条垂线相矛盾.
综上,经过一点A只能有平面α的一条垂线.
点评:本题考查经过点A只能有一条直线和平面a垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若
sinx+cosx=4-m,则实数m的取值范围是( )
| 3 |
| A、2≤m≤6 |
| B、-6≤m≤6 |
| C、2<m<6 |
| D、2≤m≤4 |
函数y=
的定义域为( )
| 1-x |
| A、{x|x≤1} |
| B、{x|x<1} |
| C、{x|x≥1} |
| D、{x|x>1} |
已知f(x)=asinx+bx+4(a,b为实数),且f(ln10)=5,则f(ln
)的值是( )
| 1 |
| 10 |
| A、-5 | B、-3 |
| C、3 | D、随a,b取不同值而取不同值 |
 一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )
一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )| A、4π | B、3π | C、2π | D、π |