题目内容

11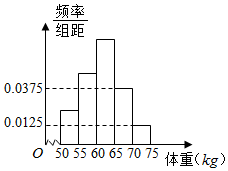．如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率依次成等差数列，第2小组的频数为10，则抽取的学生人数为40．

分析 根据题意求出前3个小组的频率和，再求第2小组的频率，从而求出样本容量．

解答 解：前3个小组的频率和为1-（0.0375+0.0125）×5=0.75，
所以第2小组的频率为$\frac{1}{3}$×0.75=0.25；
所以抽取的学生人数为：$\frac{10}{0.25}$=40．
故答案为：40．

点评 本题考查了利用频率分布直方图中的数据求对应的频率和样本容量的应用问题，也考查了等差中项的应用问题，是基础题．

练习册系列答案
相关题目
1．若数列{an}中，a1=1，an+1=2an+1（n∈N*），则数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$的各项和为1．
2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A1，A2，且|A1A2|=4，上顶点为B，若直线BA1与圆M：（x+1）2+y2=$\frac{3}{7}$相切．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）直线l：x=2$\sqrt{2}$与x轴交于D，P是椭圆C上异于A1、A2的动点，直线A1P、A2P分别交直线l于E、F两点，求证：|DE|•|DF|为定值．
19．在复平面内，复数（1+$\sqrt{3}$i）•i对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
6．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=$\frac{π}{3}$对称，则φ的最小值为（　　）
A．$\frac{5π}{12}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$
16．若函数f（x）=$\left\{\begin{array}{l}{lnx，（x＞0）}\\{{e}^{x+1}-2，（x≤0）}\end{array}\right.$，则f（f（$\frac{1}{e}$））=（　　）
A．-1B．0C．1D．3
3．若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ=$\frac{6cosθ}{si{n}^{2}θ}$．
（1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（2）若直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{3}{2}+t}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数）当直线l与曲线C相交于A，B两点，求|$\overrightarrow{AB}$|
20．已知圆C：x2+y2-4x=0，直线l：kx-3k-y=0，则直线l与圆C的位置关系是（　　）
A．相交B．相切
C．相离D．以上三种均有可能
1．已知点列${A_n}（{{a_n}，{b_n}}）（{n∈{N^*}}）$是函数y=ax（a＞0，a≠1）图象上的点，点列Bn（n，0）满足|AnBn|=|AnBn+1|，若数列{bn}中任意相邻三项能构成三角形三边，则a的取值范围是（　　）
A．$0＜a＜\frac{{\sqrt{5}-1}}{2}$或$a＞\frac{{\sqrt{5}+1}}{2}$B．$\frac{{\sqrt{5}-1}}{2}＜a＜1$或$1＜a＜\frac{{\sqrt{5}+1}}{2}$
C．$0＜a＜\frac{{\sqrt{3}-1}}{2}$或$a＞\frac{{\sqrt{3}+1}}{2}$D．$\frac{{\sqrt{3}-1}}{2}＜a＜1$或$1＜a＜\frac{{\sqrt{3}+1}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网