题目内容
8.已知a>0,且a≠1,则双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-y2=1与双曲线C2:$\frac{{y}^{2}}{{a}^{2}}$-x2=1的( )| A. | 焦点相同 | B. | 顶点相同 | C. | 渐近线相同 | D. | 离心率相等 |
分析 根据题意,由双曲线C1与C2的标准方程,分析其焦点位置,进而求出C1与C2的焦点坐标、顶点坐标、渐近线方程以及离心率,比较即可得答案.
解答 解:根据题意,双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-y2=1,其焦点在x轴上,c=$\sqrt{{a}^{2}+1}$,
则其焦点坐标为($\sqrt{{a}^{2}+1}$,0),顶点坐标(a,0),渐近线方程:y=±$\frac{1}{a}$x,离心率e=$\frac{\sqrt{{a}^{2}+1}}{a}$;
双曲线C2:$\frac{{y}^{2}}{{a}^{2}}$-x2=1,其焦点在y轴上,c=$\sqrt{{a}^{2}+1}$,
则其焦点坐标为(0,$\sqrt{{a}^{2}+1}$),顶点坐标(0,a),渐近线方程:y=±ax,离心率e=$\frac{\sqrt{{a}^{2}+1}}{a}$;
分析可得:双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-y2=1与双曲线C2:$\frac{{y}^{2}}{{a}^{2}}$-x2=1的离心率相同;
故选:D.
点评 本题考查双曲线的几何性质,注意由双曲线的方程分析双曲线的焦点位置.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.在底面是菱形的四棱锥P-ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则$\frac{AK}{PK}$等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
20.执行如图所示的程序框图,输出的S=( )
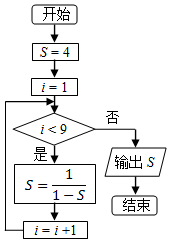

| A. | 4 | B. | $-\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
16.等差数列中{an},a1=2,公差为d,则“d=4”是“a1,a2,a5成等比数列”的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
3.已知a>b>0,c<0,下列不等关系中正确的是( )
| A. | ac>bc | B. | ac>bc | C. | loga(a-c)>logb(b-c) | D. | $\frac{a}{a-c}$>$\frac{b}{b-c}$ |
13.已知f(x)是定义在区间(0,+∞)内的单调函数,且对?x∈(0,∞),都有f[f(x)-lnx]=e+1,设f′(x)为f(x)的导函数,则函数g(x)=f(x)-f′(x)的零点个数为( )
| A. | 0 | B. | l | C. | 2 | D. | 3 |
15.直线l:kx+y+4=0(k∈R)是圆C:x2+y2+4x-4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线m,则直线m被圆C所截得的弦长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |