题目内容
1．函数y=sin（$\frac{2015}{2}$π-x）是（ ）| A． | 奇函数 | B． | 偶函数 | ||
| C． | 非奇非偶函数 | D． | 既是奇函数又是偶函数 |
分析 利用诱导公式、余弦函数的奇偶性，得出结论．
解答 解：函数y=sin（$\frac{2015}{2}$π-x）=sin（1006π+3•$\frac{π}{2}$-x）=-cosx，
故它是偶函数，
故选：B．
点评 本题主要考查诱导公式、余弦函数的奇偶性，属于基础题．
练习册系列答案
小学教材完全解读系列答案
相关题目
11．命题“对于任意角θ，cos4θ-sin4θ=cos2θ”的证明：“cos4θ-sin4θ=（cos2θ-sin2θ）（cos2θ+sin2θ）=cos2θ-sin2θ=cos2θ．”该过程应用了（ ）
| A． | 分析法 | B． | 综合法 | C． | 间接证明法 | D． | 反证法 |
12．下面表示同一集合的是（ ）
| A． | M={（1，2）}，N={（2，1）} | B． | M={1，2}，N={（2，1）} | ||
| C． | M=∅，N={∅} | D． | M={x︳x2-3x+2=0}，N={1，2} |
16．已知θ为钝角，且sinθ+cosθ=$\frac{1}{5}$，则tan2θ=（ ）
| A． | -$\frac{24}{7}$ | B． | $\frac{24}{7}$ | C． | -$\frac{7}{24}$ | D． | $\frac{7}{24}$ |
6．若sinα=-$\frac{3}{5}$，α是第三象限角，则cos（α+$\frac{π}{4}$）=（ ）
| A． | $-\frac{{7\sqrt{2}}}{10}$ | B． | $\frac{{7\sqrt{2}}}{10}$ | C． | $-\frac{{\sqrt{2}}}{10}$ | D． | $\frac{{\sqrt{2}}}{10}$ |
13．已知cos（2π-α）=$\frac{3}{4}$，α∈（-$\frac{π}{2}$，0），则sin2α的值为（ ）
| A． | $\frac{3}{8}$ | B． | $-\frac{3}{8}$ | C． | $\frac{{3\sqrt{7}}}{8}$ | D． | -$\frac{{3\sqrt{7}}}{8}$ |
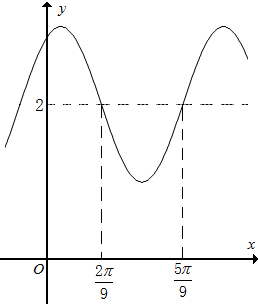函数y=Asin（ωx+φ）+2（A＞0，ω＞0，0＜φ＜2π）的图象如图所示，则ω=3，φ=$\frac{π}{3}$．