题目内容
20．（1）若C202x=C2016-x，求实数x的值；（2）已知（1+ax）3+（1-x）5的展开式中x3的系数为-2，求实数a的值．
分析 （1）由条件利用组合数公式求得x的值．
（2）把（1+ax）3 和（1-x）5 分别利用二项式定理展开，可得展开式中x3的系数，再根据展开式中x3的系数为-2，求得a的值．
解答 解：（1）C202x=C2016-x，则有2x=16-x 或2x+16-x=20，求得x=4．
（2）∵（1+ax）3 +（1-x）5=（${C}_{3}^{0}$+${C}_{3}^{1}$•（ax）+${C}_{3}^{2}$•（ax）2+${C}_{3}^{3}$•（ax）3）•（${C}_{5}^{0}$-${C}_{5}^{1}$•x+${C}_{5}^{2}$•x2-${C}_{5}^{3}$•x3+${C}_{5}^{4}$•x4-x5），
∴展开式中x3的系数为-${C}_{5}^{3}$+3a•${C}_{5}^{2}$-3a2•5+a3•${C}_{5}^{0}$=-2，即 a3-15a2+30a-8=（a-2）（a2-13a+4）=0，
求得a=2．
点评 本题主要考查组合数公式，二项式定理的应用，属于中档题．
练习册系列答案
相关题目
10．下列不等式一定成立的是（ ）
| A． | x2+$\frac{1}{4}$＞x（x＞0） | B． | x2+1≥2|x|（x∈R） | ||
| C． | sinx+$\frac{1}{sinx}$≥2（x≠kπ，k∈Z） | D． | $\frac{1}{{{x^2}+1}}$＞1（x∈R） |
11．命题“对于任意角θ，cos4θ-sin4θ=cos2θ”的证明：“cos4θ-sin4θ=（cos2θ-sin2θ）（cos2θ+sin2θ）=cos2θ-sin2θ=cos2θ．”该过程应用了（ ）
| A． | 分析法 | B． | 综合法 | C． | 间接证明法 | D． | 反证法 |
15．某位同学为了研究气温对饮料销售的影响，经过对某小卖部的统计，得到一个卖出的某种饮料杯数与当天气温的对比表．他分别记录了3月21日至3月25日的白天平均气温x（℃）与该小卖部的这种饮料销量y（杯），得到如下数据
（1）若先从这五组数据中任取2组，求取出的2组数据恰好是相邻2天数据的概率；
（2）请根据所给五组数据，求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）根据（2）中所得的线性回归方程，若天气预报3月26日的白天平均气温7（℃），请预测小卖部的这种饮料的销量．（参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
| 日 期 | 3月21日 | 3月22日 | 3月23日 | 3月24日 | 3月25日 |
| 平均气温x（°C） | 8 | 10 | 14 | 11 | 12 |
| 销量y（杯） | 21 | 25 | 35 | 26 | 28 |
（2）请根据所给五组数据，求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）根据（2）中所得的线性回归方程，若天气预报3月26日的白天平均气温7（℃），请预测小卖部的这种饮料的销量．（参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
12．下面表示同一集合的是（ ）
| A． | M={（1，2）}，N={（2，1）} | B． | M={1，2}，N={（2，1）} | ||
| C． | M=∅，N={∅} | D． | M={x︳x2-3x+2=0}，N={1，2} |
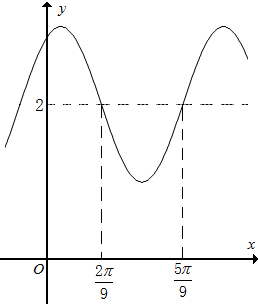函数y=Asin（ωx+φ）+2（A＞0，ω＞0，0＜φ＜2π）的图象如图所示，则ω=3，φ=$\frac{π}{3}$．