题目内容
15.已知a满足方程x+lgx=4,b满足方程x+10x=4,函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+(a+b)x+2,x≤0}\\{2,x>0}\end{array}\right.$,则关于x的方程f(x)=x的所有实数根之和是( )| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
分析 化简可得x=lg(4-x),令f(x)=x-lg(4-x),从而可得4-a=b,化简f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x+2,x≤0}\\{2,x>0}\end{array}\right.$,从而分类讨论求方程的实数根之和.
解答 解:∵x+10x=4,
∴10x=4-x,
∴x=lg(4-x),
令f(x)=x-lg(4-x),
∵a+lga-4=0,b-lg(4-b)=0,
∴4-a=b,
故a+b=4;
故f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x+2,x≤0}\\{2,x>0}\end{array}\right.$,
当x>0时,f(x)=2=x,
当x≤0时,f(x)=x2+4x+2=x,
解得,x=-1或x=-2;
故f(x)=x的根为-1,-2,0;
故关于x的方程f(x)=x的所有实数根之和是-3,
故选:C.
点评 本题考查了方程的根与函数的零点的关系应用及分类讨论的思想应用.

练习册系列答案
相关题目
6.若sinα=-$\frac{3}{5}$,α是第三象限角,则cos(α+$\frac{π}{4}$)=( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
5.在二项式(3+2x)8的展开式中,最大的二项式系数是( )
| A. | C${\;}_{8}^{3}$ | B. | ${C}_{8}^{4}$ | C. | ${C}_{8}^{5}$ | D. | ${C}_{8}^{6}$ |
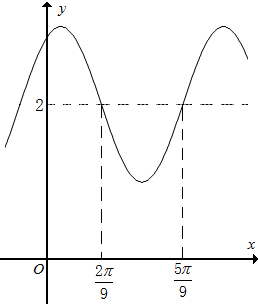 函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.
函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.