题目内容
14.已知f(x)是定义在[-1,1]上的单调递增函数,且f(1)=1.(1)解不等式f(x+$\frac{1}{2}$)<f(1-x);
(2)若f(x)≤m2-2m+1,对所有x∈[-1,1]恒成立,求实数m的取值范围.
分析 (1)由f(x)是定义在[-1,1]上的单调递增函数,不等式f(x+$\frac{1}{2}$)<f(1-x)即为-1≤x+$\frac{1}{2}$≤1,-1≤1-x≤1,x+$\frac{1}{2}$<1-x,解不等式即可得到所求解集;
(2)由题意可得f(x)的最大值为1,有1≤m2-2m+1,解不等式即可得到m的范围.
解答 解:(1)f(x)是定义在[-1,1]上的单调递增函数,
不等式f(x+$\frac{1}{2}$)<f(1-x)即为
$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$即有$\left\{\begin{array}{l}{-\frac{3}{2}≤x≤\frac{1}{2}}\\{0≤x≤2}\\{x<\frac{1}{4}}\end{array}\right.$,
解得0≤x<$\frac{1}{4}$,
即有解集为[0,$\frac{1}{4}$);
(2)f(x)是定义在[-1,1]上的单调递增函数,
且f(1)=1,则f(x)的最大值为1,
f(x)≤m2-2m+1,对所有x∈[-1,1]恒成立,
即有1≤m2-2m+1,解得m≥2或m≤0.
故实数m的取值范围是(-∞,0]∪[2,+∞).
点评 本题考查函数的单调性的运用:解不等式,注意函数定义域的运用,考查不等式恒成立问题的解法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.设a>0,且a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=3,求$\frac{{a}^{2}+{a}^{-2}+1}{a+{a}^{-1}+1}$的值.
2.下列四个函数中,既是偶函数又在(0,+∞)上为增函数的是( )
| A. | y=x2-2x | B. | y=x3 | C. | y=ln$\sqrt{1-{x}^{2}}$ | D. | y=|x|+1 |
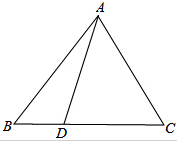 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.