题目内容
17.已知函数$f(x)=\frac{{{x^2}+a}}{x},且f(1)=2$(1)证明函数f(x)是奇函数;
(2)证明f(x)在(1,+∞)上是增函数.
分析 (1)由解析式先求出函数的定义域,化简f(x)和f(-x)后,由函数奇偶性的定义即可证明;
(2)根据函数单调性的定义:取值、作差、变形、定号、下结论,进行证明即可.
解答 (1)证明:f(x)的定义域为{x|x≠0},关于原点对称,
∵f(1)=2,∴1+a=2,即a=1
∵f(x)=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$,f(-x)=-x-$\frac{1}{x}$=-f(x),
∴f(x)是奇函数.
(2)证明:任取x1,x2∈(1,+∞)且x1<x2,
∴f(x1)-f(x2)=x1+$\frac{1}{x1}$-(x2+$\frac{1}{x2}$)
=(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$.
∵x1<x2,且x1x2∈(1,+∞),
∴x1-x2<0,x1x2>1,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(1,+∞)上为增函数.
点评 本题考查函数奇偶性的定义,函数单调性的定义:取值、作差、变形、定号、下结论的应用,考查化简、变形能力,属于中档题.

练习册系列答案
相关题目
7.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别F1(-c,0),F2(c,0),若椭圆上存在点P,使得csin∠PF1F2=asin∠PF2F1≠0,则离心率e的取值范围是( )
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\sqrt{2}-1,1)$ | C. | $[\sqrt{2}-1,1)$ | D. | $(0,\sqrt{2}-1]$ |
12.在△ABC中,a,b,c为角A,B,C的对边,若b=1,c=$\sqrt{3}$,A=$\frac{π}{6}$,则cos5B=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-1 | D. | -$\frac{\sqrt{3}}{2}$或0 |
2.若集合M={x∈Z||x|≤2},N={x|x2+2x-3<0},则M∩N=( )
| A. | [-2,1) | B. | [-2,1] | C. | {-2,-1,0} | D. | {-1,0} |
9.已知a,b,c满足4a=9,b=log${\;}_{\frac{1}{3}}$5,c3=$\frac{3}{5}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
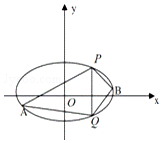 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.