题目内容
18.设二阶矩阵A,B满足A-1=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$,BA=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,求矩阵B的特征值.分析 由题意知BAA-1=EA-1⇒B=A-1,所以矩阵B的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{-3}&{λ-2}\end{array}|$=λ2-3λ-4;
解答 解:∵BA=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,∴BAA-1=EA-1⇒B=A-1;
∵A-1=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$,∴B=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$;
∴矩阵B的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{-3}&{λ-2}\end{array}|$=λ2-3λ-4;
由f(λ)=0,解得λ1=-1,λ2=4;
∴矩阵B的特征值为-1和4.
点评 本题主要考查了矩阵与逆矩阵之间的关系,以及特征多项式的求法,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.在△ABC中,a=$\sqrt{3}$b,A=120°,则B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.关于函数f(x)=log${\;}_{\frac{1}{2}}$(1-2x)的单调性,叙述正确的是( )
| A. | f(x)在($\frac{1}{2}$,+∞)内是增函数 | B. | f(x)在($\frac{1}{2}$,+∞)内是减函数 | ||
| C. | f(x)在(-∞,$\frac{1}{2}$)内是增函数 | D. | f(x)在(-∞,$\frac{1}{2}$)内是减函数 |
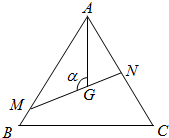 如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.