题目内容

6．若函数$f（x）=1+\frac{2}{x-1}$，x∈[2，4），则f（x）的值域是（$\frac{5}{3}$，3]．

分析 根据反比例函数的性质，利用单调性求解即可．

解答 解：函数$f（x）=1+\frac{2}{x-1}$，
∵y=$\frac{2}{x-1}$在（-∞，1）和（1，+∞）是单调递减，
∴y=$\frac{2}{x-1}$在，x∈[2，4）的值域为y∈（$\frac{2}{3}$，2]，
∴函数$f（x）=1+\frac{2}{x-1}$在x∈[2，4）上的值域为（$\frac{5}{3}$，3]
故答案为：（$\frac{5}{3}$，3]．

点评 本题考查了值域的求法，利用了函数的单调性求解．比较基础．

练习册系列答案
相关题目
16．在平面直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立坐标系，曲线C1的参数方程为$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．
（1）求曲线C1的直角坐标方程；
（2）曲线C2的极坐标方程为θ=$\frac{π}{6}$（ρ∈R），求C1与C2的公共点的极坐标．
17．已知函数$f（x）=\frac{{{x^2}+a}}{x}，且f（1）=2$
（1）证明函数f（x）是奇函数；
（2）证明f（x）在（1，+∞）上是增函数．
14．直线$\left\{{\begin{array}{l}{x=3+tcos{{230}°}\;\;}\\{y=-1+tsin{{230}°}}\end{array}}\right.$（t为参数）的倾斜角是（　　）
A．30°B．45°C．50°D．60°
1．已知m，n是不重合的两条直线，α，β是不重合的两个平面．下列命题：
①若α⊥β，m⊥α，则m∥β；
②若m⊥α，m⊥β，则α∥β；
③若m∥α，n⊥α，则m⊥n；
④若m∥α，m?β，则α∥β．
其中所有真命题的序号是②③．
11．德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数f（x）=$\left\{\begin{array}{l}1，x为有理数\\ 0，x为无理数\end{array}$，称为狄利克雷函数，则关于函数f（x）有以下四个命题：
①f（f（x））=1；
②函数f（x）是偶函数；
③任意一个非零有理数T，f（x+T）=f（x）对任意x∈R恒成立；
④存在三个点A（x1，f（x1）），B（x2，f（x2）），C（x3，f（x3）），使得△ABC为等边三角形．
其中真命题的个数是（　　）
A．4B．3C．2D．1
18．中国人口已经出现老龄化与少子化并存的结构特征，测算显示中国是世界上人口老龄化速度最快的国家之一，再不实施“放开二胎”新政策，整个社会将会出现一系列的问题，若某地区2015年人口总数为45万，实施“放开二胎”新政策后专家估计人口总数将发生如下变化：从2016年开始到2025年每年人口比上年增加0.5万人，从2026年开始到2035年每年人口为上一年的99%．
（1）求实施新政策后，从2016年开始到2035年，第n年的人口总数an的表达式；
（2）若新政策实施后的2016年到2035年人口平均值超过49万，则需调整政策，否则继续实施，问到2035年后是否需要调整政策？（说明：0.9910=（1-001）10≈0.9）．
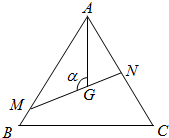6．如图，是△ABC边长为1的正三角形，M，N分别是AB，AC边上的点，线段MN过△ABC的重心，设∠MGA=α，$\frac{π}{3}$≤α≤$\frac{2π}{3}$．
（Ⅰ）当α=$\frac{2π}{3}$时，求MG的长；
（Ⅱ）分别记△AGM，△AGN的面积为S1，S2，试将S1，S2表示为α的函数；
（Ⅲ）设y=$\frac{1}{{{S}_{1}}^{2}}$+$\frac{1}{{{S}_{2}}^{2}}$，求y的最小值．
7．各项均为正数的数列{an}中，前n项和${S_n}={（{\frac{{{a_n}+1}}{2}}）^2}$．
（1）求数列{an}的通项公式；
（2）若$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$＜k恒成立，求k的取值范围；
（3）是否存在正整数m，k，使得am，am+5，ak成等比数列？若存在，求出m和k的值，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网