题目内容
20.在($\frac{{\sqrt{x}}}{2}$-$\frac{2}{{\sqrt{x}}}$)4的二项展开式中,x的系数为( )| A. | -$\frac{15}{4}$ | B. | -$\frac{3}{8}$ | C. | $\frac{15}{4}$ | D. | -1 |
分析 根据二项展开式的通项公式,令展开式的含x项的指数为1,即可求出展开式中x项的系数.
解答 解:($\frac{{\sqrt{x}}}{2}$-$\frac{2}{{\sqrt{x}}}$)4的二项展开式中,通项公式为
Tr+1=(-1)r•${C}_{4}^{r}$•($\frac{\sqrt{x}}{2}$)4-r•($\frac{2}{\sqrt{x}}$)r=(-1)r•${C}_{4}^{r}$•22r-4•x2-r;
令2-r=1,可得r=1,
∴展开式中x项的系数是(-1)•${C}_{4}^{1}$•2-2=-1.
故选:D.
点评 本题考查了二项式展开式的通项公式的应用问题,是基础题目.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
10.已知命题p:函数y=ln(x2+3)+$\frac{1}{{ln({x^2}+3)}}$的最小值是2;命题q:x>2是x>l的充分不必要条件.则下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
12.已知集合A={x∈R|-1<x<3},B={x∈R|-1<x<m+1},若x∈B成立的一个充分不必要条件是x∈A,则实数m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
9.随机变量ξ的分布列如表,则D(ξ)=$\frac{5}{9}$
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
10.直线2xcosθ-y-3=0(θ∈[$\frac{π}{6}$,$\frac{π}{3}$])的斜率的变化范围是( )
| A. | [$\frac{{\sqrt{3}}}{3}$,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | [1,+∞) | D. | (-∞,-$\sqrt{3}$] |
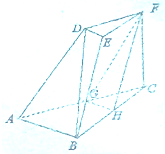 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.