题目内容
10.已知命题p:函数y=ln(x2+3)+$\frac{1}{{ln({x^2}+3)}}$的最小值是2;命题q:x>2是x>l的充分不必要条件.则下列命题为真命题的是( )| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
分析 分别判断p,q的真假,从而判断出复合命题的真假.
解答 解:y=ln(x2+3)+$\frac{1}{{ln({x^2}+3)}}$>2$\sqrt{ln{(x}^{2}+3)•\frac{1}{ln{(x}^{2}+3)}}$=2,
令ln(x2+3)=$\frac{1}{ln{(x}^{2}+3)}$,得:ln(x2+3)=1,
显然ln(x2+3)>lne=1,故“=”不成立,取不到2,
故命题p是假命题;
x>2是x>l的充分不必要条件,
故命题q是真命题,
故?p∧q是真命题,
故选:C.
点评 本题考查了对数函数的性质,考查充分必要条件,考查复合命题的判断,是一道基础题.

练习册系列答案
相关题目
2.若x≠y,且x,a1,a2,a3,y与x,b1,b2,b3,b4,y各成等差数列,则$\frac{{a}_{2}-{a}_{1}}{{b}_{2}-{b}_{1}}$的值为( )
| A. | 1 | B. | $\frac{4}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
20.在($\frac{{\sqrt{x}}}{2}$-$\frac{2}{{\sqrt{x}}}$)4的二项展开式中,x的系数为( )
| A. | -$\frac{15}{4}$ | B. | -$\frac{3}{8}$ | C. | $\frac{15}{4}$ | D. | -1 |
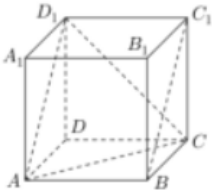 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: