题目内容
19.已知函数f(x)=xα,当x∈(1,+∞)时,f(x)-x<0,则( )| A. | 0<α<1 | B. | α<1 | C. | α>0 | D. | α<0 |
分析 令g(x)=f(x)-x=xa-x,x∈(1,+∞),可求g’(x)=axa-1-1,可证a<1,分类讨论当a≤0时,当1>a>0时,证明g(x)<0都成立即可得解.
解答 解:令g(x)=f(x)-x=xa-x,x∈(1,+∞),
则g’(x)=axa-1-1,
若a>1,则xa-1 必大于x0=1,此时必有g’(x)>0,
g(x)单调递增.g(x)>g(1)=0,
所以:a≤1.
若a=1,那么g(x)=0,舍去.
a≤0时,显然g’(x)<0,
所以:g(x)在定义域单调递减.g(x)无限接近但小于g(1)=0,成立.
1>a>0时,0<xa-1<1,那么0<axa-1<1,那么g’(x)<0恒成立,同理g(x)<0成立.
所以a<1.
故选:B.
点评 本题主要考查了指数函数的图象和性质,考查了导数的概念及其应用,考查了转化思想和分类讨论思想的应用,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
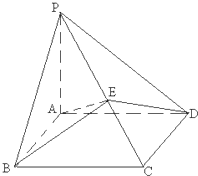 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.