题目内容
4.已知函数y=f(x)是定义在R上的偶函数,满足f(2+x)=f(2-x),若函数y=f(x)在(0,4)上至少有一个零点,且f(0)=0,则函数y=f(x)在(-8,10]上的零点个数至少为9.分析 判断f(x)的对称性和周期性,利用周期性和对称性得出答案.
解答 解:∵f(2+x)=f(2-x)=f(x-2),
∴f(x)周期为4,
∵f(0)=0,∴f(4)=f(8)=f(-4)=0,
∵f(x)在(0,4)上至少有1个零点,
∴f(x)在(-8,-4),(-4,0),(4,8)上至少有1个零点,
∵f(2+x)=f(2-x),∴f(x)关于直线x=2对称,
∴f(x)关于直线x=10对称,
∴f(x)在(8,10]上至少存在1个零点,
综上,f(x)在(-8,10]上至少存在9个零点.
故答案为:9.
点评 本题考查了函数的对称性与周期性的应用,属于中档题.

练习册系列答案
相关题目
17.1340°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
15.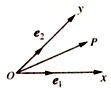 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
2.为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
| 社团名称 | 成员人数 | 抽取人数 |
| 话剧社 | 50 | a |
| 创客社 | 150 | b |
| 演讲社 | 100 | c |
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.